What is Lean
Lean is a functional programming language that makes it easy to write correct and maintainable code. You can also use Lean as an interactive theorem prover.
Lean programming primarily involves defining types and functions. This allows your focus to remain on the problem domain and manipulating its data, rather than the details of programming.
-- Defines a function that takes a name and produces a greeting.
def getGreeting (name : String) := s!"Hello, {name}! Isn't Lean great?"
-- The `main` function is the entry point of your program.
-- Its type is `IO Unit` because it can perform `IO` operations (side effects).
def main : IO Unit :=
-- Define a list of names
let names := ["Sebastian", "Leo", "Daniel"]
-- Map each name to a greeting
let greetings := names.map getGreeting
-- Print the list of greetings
for greeting in greetings do
IO.println greeting
Lean has numerous features, including:
- Type inference
- First-class functions
- Powerful data types
- Pattern matching
- Type classes
- Monads
- Extensible syntax
- Hygienic macros
- Dependent types
- Metaprogramming
- Multithreading
- Verification: you can prove properties of your functions using Lean itself
Tour of Lean
The best way to learn about Lean is to read and write Lean code. This article will act as a tour through some of the key features of the Lean language and give you some code snippets that you can execute on your machine. To learn about setting up a development environment, check out Setting Up Lean.
There are two primary concepts in Lean: functions and types. This tour will emphasize features of the language which fall into these two concepts.
Functions and Namespaces
The most fundamental pieces of any Lean program are functions organized into namespaces.
Functions perform work on inputs to produce outputs,
and they are organized under namespaces,
which are the primary way you group things in Lean.
They are defined using the def command,
which give the function a name and define its arguments.
namespace BasicFunctions
-- The `#eval` command evaluates an expression on the fly and prints the result.
#eval 2+2
-- You use 'def' to define a function. This one accepts a natural number
-- and returns a natural number.
-- Parentheses are optional for function arguments, except for when
-- you use an explicit type annotation.
-- Lean can often infer the type of the function's arguments.
def sampleFunction1 x := x*x + 3
-- Apply the function, naming the function return result using 'def'.
-- The variable type is inferred from the function return type.
def result1 := sampleFunction1 4573
-- This line uses an interpolated string to print the result. Expressions inside
-- braces `{}` are converted into strings using the polymorphic method `toString`
#eval println! "The result of squaring the integer 4573 and adding 3 is {result1}"
-- When needed, annotate the type of a parameter name using '(argument : type)'.
def sampleFunction2 (x : Nat) := 2*x*x - x + 3
def result2 := sampleFunction2 (7 + 4)
#eval println! "The result of applying the 2nd sample function to (7 + 4) is {result2}"
-- Conditionals use if/then/else
def sampleFunction3 (x : Int) :=
if x > 100 then
2*x*x - x + 3
else
2*x*x + x - 37
#eval println! "The result of applying sampleFunction3 to 2 is {sampleFunction3 2}"
end BasicFunctions
-- Lean has first-class functions.
-- `twice` takes two arguments `f` and `a` where
-- `f` is a function from natural numbers to natural numbers, and
-- `a` is a natural number.
def twice (f : Nat → Nat) (a : Nat) :=
f (f a)
-- `fun` is used to declare anonymous functions
#eval twice (fun x => x + 2) 10
-- You can prove theorems about your functions.
-- The following theorem states that for any natural number `a`,
-- adding 2 twice produces a value equal to `a + 4`.
theorem twiceAdd2 (a : Nat) : twice (fun x => x + 2) a = a + 4 :=
-- The proof is by reflexivity. Lean "symbolically" reduces both sides of the equality
-- until they are identical.
rfl
-- `(· + 2)` is syntax sugar for `(fun x => x + 2)`. The parentheses + `·` notation
-- is useful for defining simple anonymous functions.
#eval twice (· + 2) 10
-- Enumerated types are a special case of inductive types in Lean,
-- which we will learn about later.
-- The following command creates a new type `Weekday`.
inductive Weekday where
| sunday : Weekday
| monday : Weekday
| tuesday : Weekday
| wednesday : Weekday
| thursday : Weekday
| friday : Weekday
| saturday : Weekday
-- `Weekday` has 7 constructors/elements.
-- The constructors live in the `Weekday` namespace.
-- Think of `sunday`, `monday`, …, `saturday` as being distinct elements of `Weekday`,
-- with no other distinguishing properties.
-- The command `#check` prints the type of a term in Lean.
#check Weekday.sunday
#check Weekday.monday
-- The `open` command opens a namespace, making all declarations in it accessible without
-- qualification.
open Weekday
#check sunday
#check tuesday
-- You can define functions by pattern matching.
-- The following function converts a `Weekday` into a natural number.
def natOfWeekday (d : Weekday) : Nat :=
match d with
| sunday => 1
| monday => 2
| tuesday => 3
| wednesday => 4
| thursday => 5
| friday => 6
| saturday => 7
#eval natOfWeekday tuesday
def isMonday : Weekday → Bool :=
-- `fun` + `match` is a common idiom.
-- The following expression is syntax sugar for
-- `fun d => match d with | monday => true | _ => false`.
fun
| monday => true
| _ => false
#eval isMonday monday
#eval isMonday sunday
-- Lean has support for type classes and polymorphic methods.
-- The `toString` method converts a value into a `String`.
#eval toString 10
#eval toString (10, 20)
-- The method `toString` converts values of any type that implements
-- the class `ToString`.
-- You can implement instances of `ToString` for your own types.
instance : ToString Weekday where
toString (d : Weekday) : String :=
match d with
| sunday => "Sunday"
| monday => "Monday"
| tuesday => "Tuesday"
| wednesday => "Wednesday"
| thursday => "Thursday"
| friday => "Friday"
| saturday => "Saturday"
#eval toString (sunday, 10)
def Weekday.next (d : Weekday) : Weekday :=
match d with
| sunday => monday
| monday => tuesday
| tuesday => wednesday
| wednesday => thursday
| thursday => friday
| friday => saturday
| saturday => sunday
#eval Weekday.next Weekday.wednesday
-- Since the `Weekday` namespace has already been opened, you can also write
#eval next wednesday
-- Matching on a parameter like in the previous definition
-- is so common that Lean provides syntax sugar for it. The following
-- function uses it.
def Weekday.previous : Weekday -> Weekday
| sunday => saturday
| monday => sunday
| tuesday => monday
| wednesday => tuesday
| thursday => wednesday
| friday => thursday
| saturday => friday
#eval next (previous wednesday)
-- We can prove that for any `Weekday` `d`, `next (previous d) = d`
theorem Weekday.nextOfPrevious (d : Weekday) : next (previous d) = d :=
match d with
| sunday => rfl
| monday => rfl
| tuesday => rfl
| wednesday => rfl
| thursday => rfl
| friday => rfl
| saturday => rfl
-- You can automate definitions such as `Weekday.nextOfPrevious`
-- using metaprogramming (or "tactics").
theorem Weekday.nextOfPrevious' (d : Weekday) : next (previous d) = d := by
cases d -- A proof by case distinction
all_goals rfl -- Each case is solved using `rfl`
Quickstart
These instructions will walk you through setting up Lean 4 together with VS Code as an editor for Lean 4. See Setup for supported platforms and other ways to set up Lean 4.
-
Install VS Code.
-
Launch VS Code and install the
Lean 4extension by clicking on the 'Extensions' sidebar entry and searching for 'Lean 4'.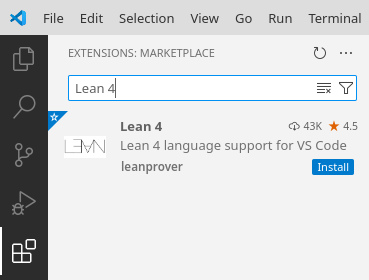
-
Open the Lean 4 setup guide by creating a new text file using 'File > New Text File' (
Ctrl+N/Cmd+N), clicking on the ∀-symbol in the top right and selecting 'Documentation… > Docs: Show Setup Guide'.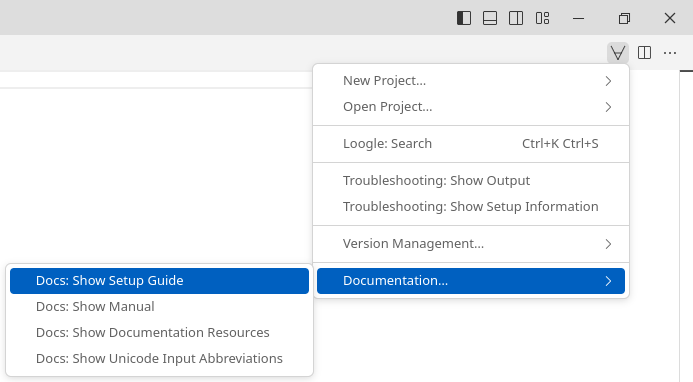
-
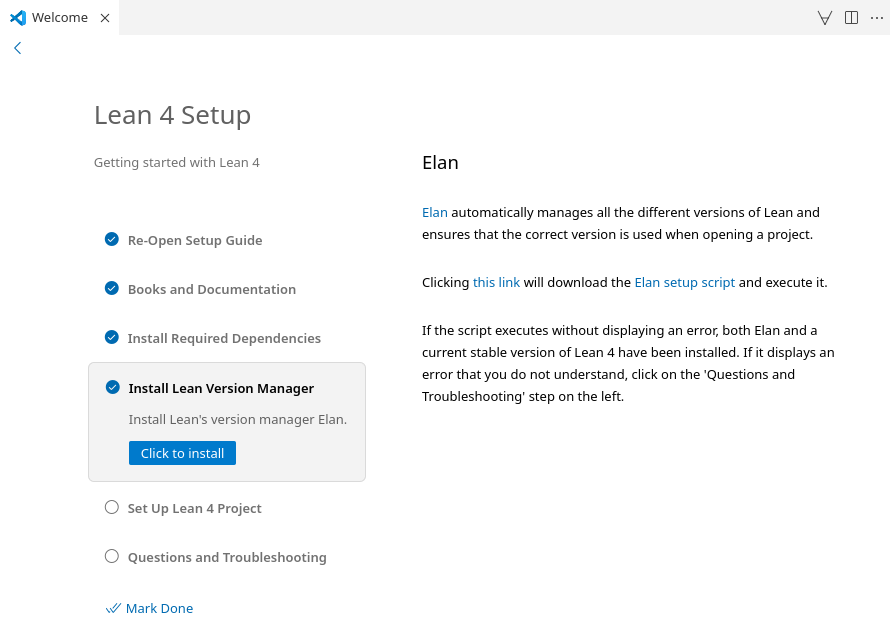
Follow the Lean 4 setup guide. It will:
- walk you through learning resources for Lean,
- teach you how to set up Lean's dependencies on your platform,
- install Lean 4 for you at the click of a button,
- help you set up your first project.
Supported Platforms
Tier 1
Platforms built & tested by our CI, available as binary releases via elan (see below)
- x86-64 Linux with glibc 2.26+
- x86-64 macOS 10.15+
- aarch64 (Apple Silicon) macOS 10.15+
- x86-64 Windows 11 (any version), Windows 10 (version 1903 or higher), Windows Server 2022, Windows Server 2025
Tier 2
Platforms cross-compiled but not tested by our CI, available as binary releases
Releases may be silently broken due to the lack of automated testing. Issue reports and fixes are welcome.
- aarch64 Linux with glibc 2.27+
- x86 (32-bit) Linux
- Emscripten Web Assembly
Setting Up Lean
See also the quickstart instructions for a standard setup with VS Code as the editor.
Release builds for all supported platforms are available at https://github.com/leanprover/lean4/releases.
Instead of downloading these and setting up the paths manually, however, it is recommended to use the Lean version manager elan instead:
$ elan self update # in case you haven't updated elan in a while
# download & activate latest Lean 4 stable release (https://github.com/leanprover/lean4/releases)
$ elan default leanprover/lean4:stable
lake
Lean 4 comes with a package manager named lake.
Use lake init foo to initialize a Lean package foo in the current directory, and lake build to typecheck and build it as well as all its dependencies. Use lake help to learn about further commands.
The general directory structure of a package foo is
lakefile.lean # package configuration
lean-toolchain # specifies the lean version to use
Foo.lean # main file, import via `import Foo`
Foo/
A.lean # further files, import via e.g. `import Foo.A`
A/... # further nesting
.lake/ # `lake` build output directory
After running lake build you will see a binary named ./.lake/build/bin/foo and when you run it you should see the output:
Hello, world!
Editing
Lean implements the Language Server Protocol that can be used for interactive development in Emacs, VS Code, and possibly other editors.
Changes must be saved to be visible in other files, which must then be invalidated using an editor command (see links above).
Theorem Proving in Lean
We strongly encourage you to read the book Theorem Proving in Lean. Many Lean users consider it to be the Lean Bible.
Functional Programming in Lean
The goal of this book is to be an accessible introduction to using Lean 4 as a programming language. It should be useful both to people who want to use Lean as a general-purpose programming language and to mathematicians who want to develop larger-scale proof automation but do not have a background in functional programming. It does not assume any background with functional programming, though it's probably not a good first book on programming in general. New content will be added once per month until it's done.
Examples
- Palindromes
- Binary Search Trees
- A Certified Type Checker
- The Well-Typed Interpreter
- Dependent de Bruijn Indices
- Parametric Higher-Order Abstract Syntax
Palindromes
Palindromes are lists that read the same from left to right and from right to left.
For example, [a, b, b, a] and [a, h, a] are palindromes.
We use an inductive predicate to specify whether a list is a palindrome or not.
Recall that inductive predicates, or inductively defined propositions, are a convenient
way to specify functions of type ... → Prop.
This example is a based on an example from the book "The Hitchhiker's Guide to Logical Verification".
inductive Palindrome: {α : Type u_1} → List α → Prop
Palindrome : List: Type u_1 → Type u_1
List α: Type u_1
α → Prop: Type
Prop where
| nil: ∀ {α : Type u_1}, Palindrome []
nil : Palindrome: {α : Type u_1} → List α → Prop
Palindrome []: List ?m.17
[]
| single: ∀ {α : Type u_1} (a : α), Palindrome [a]
single : (a: α
a : α: Type u_1
α) → Palindrome: {α : Type u_1} → List α → Prop
Palindrome [a: α
a]
| sandwich: ∀ {α : Type u_1} {as : List α} (a : α), Palindrome as → Palindrome ([a] ++ as ++ [a])
sandwich : (a: α
a : α: Type u_1
α) → Palindrome: {α : Type u_1} → List α → Prop
Palindrome as: List α
as → Palindrome: {α : Type u_1} → List α → Prop
Palindrome ([a: α
a] ++ as: List α
as ++ [a: α
a])
The definition distinguishes three cases: (1) [] is a palindrome; (2) for any element
a, the singleton list [a] is a palindrome; (3) for any element a and any palindrome
[b₁, . . ., bₙ], the list [a, b₁, . . ., bₙ, a] is a palindrome.
We now prove that the reverse of a palindrome is a palindrome using induction on the inductive predicate h : Palindrome as.
Goals accomplished! 🐙α✝: Type u_1
as: List α✝
h: Palindrome asPalindrome as.reverseGoals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙;α✝: Type u_1
as, as✝: List α✝
a: α✝
h: Palindrome as✝
ih: Palindrome as✝.reverse
sandwichPalindrome (a :: (as✝.reverse ++ [a]))Goals accomplished! 🐙
If a list as is a palindrome, then the reverse of as is equal to itself.
Goals accomplished! 🐙α✝: Type u_1
as: List α✝
h: Palindrome asas.reverse = asGoals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙
Note that you can also easily prove palindrome_reverse using reverse_eq_of_palindrome.
Goals accomplished! 🐙Goals accomplished! 🐙
Given a nonempty list, the function List.last returns its element.
Note that we use (by simp) to prove that a₂ :: as ≠ [] in the recursive application.
defList.last : (List.last: {α : Type u_1} → (as : List α) → as ≠ [] → αas :as: List αListList: Type u_1 → Type u_1α) →α: Type u_1as ≠as: List α[] →[]: List αα | [α: Type u_1a], _ =>a: αa | _::a: αa₂::a₂: αas, _ => (as: List αa₂::a₂: αas).as: List αlast (last: {α : Type u_1} → (as : List α) → as ≠ [] → αGoals accomplished! 🐙)Goals accomplished! 🐙
We use the function List.last to prove the following theorem that says that if a list as is not empty,
then removing the last element from as and appending it back is equal to as.
We use the attribute @[simp] to instruct the simp tactic to use this theorem as a simplification rule.
@[simp]Goals accomplished! 🐙α✝: Type u_1
as: List α✝
h: as ≠ []as.dropLast ++ [as.last h] = asα✝: Type u_1
as: List α✝
h: [] ≠ [][].dropLast ++ [[].last h] = []Goals accomplished! 🐙α✝: Type u_1
as: List α✝
a: α✝
h: [a] ≠ [][a].dropLast ++ [[a].last h] = [a]Goals accomplished! 🐙α✝: Type u_1
as✝: List α✝
a₁, a₂: α✝
as: List α✝
h: a₁ :: a₂ :: as ≠ [](a₁ :: a₂ :: as).dropLast ++ [(a₁ :: a₂ :: as).last h] = a₁ :: a₂ :: asα✝: Type u_1
as✝: List α✝
a₁, a₂: α✝
as: List α✝
h: a₁ :: a₂ :: as ≠ [](a₂ :: as).dropLast ++ [(a₂ :: as).last ⋯] = a₂ :: asα✝: Type u_1
as✝: List α✝
a₁, a₂: α✝
as: List α✝
h: a₁ :: a₂ :: as ≠ [](a₂ :: as).dropLast ++ [(a₂ :: as).last ⋯] = a₂ :: asGoals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙
We now define the following auxiliary induction principle for lists using well-founded recursion on as.length.
We can read it as follows, to prove motive as, it suffices to show that: (1) motive []; (2) motive [a] for any a;
(3) if motive as holds, then motive ([a] ++ as ++ [b]) also holds for any a, b, and as.
Note that the structure of this induction principle is very similar to the Palindrome inductive predicate.
Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙this: [a₁] ++ (a₂ :: as').dropLast ++ [(a₂ :: as').last ⋯] = a₁ :: a₂ :: as'
We use our new induction principle to prove that if as.reverse = as, then Palindrome as holds.
Note that we use the using modifier to instruct the induction tactic to use this induction principle
instead of the default one for lists.
Goals accomplished! 🐙α✝: Type u_1
h: [].reverse = []
h₁Palindrome []α✝: Type u_1
a✝: α✝
h: [a✝].reverse = [a✝]Palindrome [a✝]α✝: Type u_1
a✝¹, b✝: α✝
as✝: List α✝
a✝: as✝.reverse = as✝ → Palindrome as✝
h: ([a✝¹] ++ as✝ ++ [b✝]).reverse = [a✝¹] ++ as✝ ++ [b✝]Palindrome ([a✝¹] ++ as✝ ++ [b✝])α✝: Type u_1
h: [].reverse = []
h₁Palindrome []α✝: Type u_1
a✝: α✝
h: [a✝].reverse = [a✝]Palindrome [a✝]α✝: Type u_1
a✝¹, b✝: α✝
as✝: List α✝
a✝: as✝.reverse = as✝ → Palindrome as✝
h: ([a✝¹] ++ as✝ ++ [b✝]).reverse = [a✝¹] ++ as✝ ++ [b✝]Palindrome ([a✝¹] ++ as✝ ++ [b✝])Goals accomplished! 🐙α✝: Type u_1
a✝: α✝
h: [a✝].reverse = [a✝]
h₂Palindrome [a✝]α✝: Type u_1
a✝¹, b✝: α✝
as✝: List α✝
a✝: as✝.reverse = as✝ → Palindrome as✝
h: ([a✝¹] ++ as✝ ++ [b✝]).reverse = [a✝¹] ++ as✝ ++ [b✝]Palindrome ([a✝¹] ++ as✝ ++ [b✝])Goals accomplished! 🐙α✝: Type u_1
a✝¹, b✝: α✝
as✝: List α✝
a✝: as✝.reverse = as✝ → Palindrome as✝
h: ([a✝¹] ++ as✝ ++ [b✝]).reverse = [a✝¹] ++ as✝ ++ [b✝]
h₃Palindrome ([a✝¹] ++ as✝ ++ [b✝])α✝: Type u_1
a, b: α✝
as: List α✝
ih: as.reverse = as → Palindrome as
h: ([a] ++ as ++ [b]).reverse = [a] ++ as ++ [b]Palindrome ([a] ++ as ++ [b])Goals accomplished! 🐙Goals accomplished! 🐙α✝: Type u_1
a: α✝
as: List α✝
ih: as.reverse = as → Palindrome as
h: ([a] ++ as ++ [a]).reverse = [a] ++ as ++ [a]Palindrome ([a] ++ as ++ [a])α✝: Type u_1
a: α✝
as: List α✝
ih: as.reverse = as → Palindrome as
h: ([a] ++ as ++ [a]).reverse = [a] ++ as ++ [a]Palindrome ([a] ++ as ++ [a])Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙
We now define a function that returns true iff as is a palindrome.
The function assumes that the type α has decidable equality. We need this assumption
because we need to compare the list elements.
def List.isPalindrome: {α : Type u_1} → [DecidableEq α] → List α → Bool
List.isPalindrome [DecidableEq: Type u_1 → Type (max 0 u_1)
DecidableEq α: Type u_1
α] (as: List α
as : List: Type u_1 → Type u_1
List α: Type u_1
α) : Bool: Type
Bool :=
as: List α
as.reverse: {α : Type u_1} → List α → List α
reverse = as: List α
as
It is straightforward to prove that isPalindrome is correct using the previously proved theorems.
Goals accomplished! 🐙α: Type u_1
inst✝: DecidableEq α
as: List αas.reverse = as ↔ Palindrome asGoals accomplished! 🐙[1,1: Nat2,2: Nat1].1: NatisPalindromeisPalindrome: {α : Type} → [DecidableEq α] → List α → Bool[1,1: Nat2,2: Nat3,3: Nat1].1: NatisPalindromeisPalindrome: {α : Type} → [DecidableEq α] → List α → Bool
Binary Search Trees
If the type of keys can be totally ordered -- that is, it supports a well-behaved ≤ comparison --
then maps can be implemented with binary search trees (BSTs). Insert and lookup operations on BSTs take time
proportional to the height of the tree. If the tree is balanced, the operations therefore take logarithmic time.
This example is based on a similar example found in the "Software Foundations" book (volume 3).
We use Nat as the key type in our implementation of BSTs,
since it has a convenient total order with lots of theorems and automation available.
We leave as an exercise to the reader the generalization to arbitrary types.
inductive Tree: Type v → Type v
Tree (β: Type v
β : Type v: Type (v + 1)
Type v) where
| leaf: {β : Type v} → Tree β
leaf
| node: {β : Type v} → Tree β → Nat → β → Tree β → Tree β
node (left: Tree β
left : Tree: Type v → Type v
Tree β: Type v
β) (key: Nat
key : Nat: Type
Nat) (value: β
value : β: Type v
β) (right: Tree β
right : Tree: Type v → Type v
Tree β: Type v
β)
deriving Repr: Type u → Type u
Repr
The function contains returns true iff the given tree contains the key k.
defTree.contains (Tree.contains: {β : Type u_1} → Tree β → Nat → Boolt :t: Tree βTreeTree: Type u_1 → Type u_1β) (β: Type u_1k :k: NatNat) :Nat: TypeBool := matchBool: Typet with |t: Tree βleaf =>leaf: {β : Type ?u.1393} → Tree βfalse |false: Boolnodenode: {β : Type ?u.1402} → Tree β → Nat → β → Tree β → Tree βleftleft: Tree βkeykey: Natright => ifright: Tree βk <k: Natkey thenkey: Natleft.left: Tree βcontainscontains: {β : Type u_1} → Tree β → Nat → Boolk else ifk: Natkey <key: Natk thenk: Natright.right: Tree βcontainscontains: {β : Type u_1} → Tree β → Nat → Boolk elsek: Nattruetrue: Bool
t.find? k returns some v if v is the value bound to key k in the tree t. It returns none otherwise.
def Tree.find?: {β : Type u_1} → Tree β → Nat → Option β
Tree.find? (t: Tree β
t : Tree: Type u_1 → Type u_1
Tree β: Type u_1
β) (k: Nat
k : Nat: Type
Nat) : Option: Type u_1 → Type u_1
Option β: Type u_1
β :=
match t: Tree β
t with
| leaf: {β : Type ?u.1695} → Tree β
leaf => none: {α : Type u_1} → Option α
none
| node: {β : Type ?u.1707} → Tree β → Nat → β → Tree β → Tree β
node left: Tree β
left key: Nat
key value: β
value right: Tree β
right =>
if k: Nat
k < key: Nat
key then
left: Tree β
left.find?: {β : Type u_1} → Tree β → Nat → Option β
find? k: Nat
k
else if key: Nat
key < k: Nat
k then
right: Tree β
right.find?: {β : Type u_1} → Tree β → Nat → Option β
find? k: Nat
k
else
some: {α : Type u_1} → α → Option α
some value: β
value
t.insert k v is the map containing all the bindings of t along with a binding of k to v.
def Tree.insert: {β : Type u_1} → Tree β → Nat → β → Tree β
Tree.insert (t: Tree β
t : Tree: Type u_1 → Type u_1
Tree β: Type u_1
β) (k: Nat
k : Nat: Type
Nat) (v: β
v : β: Type u_1
β) : Tree: Type u_1 → Type u_1
Tree β: Type u_1
β :=
match t: Tree β
t with
| leaf: {β : Type ?u.2005} → Tree β
leaf => node: {β : Type u_1} → Tree β → Nat → β → Tree β → Tree β
node leaf: {β : Type u_1} → Tree β
leaf k: Nat
k v: β
v leaf: {β : Type u_1} → Tree β
leaf
| node: {β : Type ?u.2020} → Tree β → Nat → β → Tree β → Tree β
node left: Tree β
left key: Nat
key value: β
value right: Tree β
right =>
if k: Nat
k < key: Nat
key then
node: {β : Type u_1} → Tree β → Nat → β → Tree β → Tree β
node (left: Tree β
left.insert: {β : Type u_1} → Tree β → Nat → β → Tree β
insert k: Nat
k v: β
v) key: Nat
key value: β
value right: Tree β
right
else if key: Nat
key < k: Nat
k then
node: {β : Type u_1} → Tree β → Nat → β → Tree β → Tree β
node left: Tree β
left key: Nat
key value: β
value (right: Tree β
right.insert: {β : Type u_1} → Tree β → Nat → β → Tree β
insert k: Nat
k v: β
v)
else
node: {β : Type u_1} → Tree β → Nat → β → Tree β → Tree β
node left: Tree β
left k: Nat
k v: β
v right: Tree β
right
Let's add a new operation to our tree: converting it to an association list that contains the key--value bindings from the tree stored as pairs. If that list is sorted by the keys, then any two trees that represent the same map would be converted to the same list. Here's a function that does so with an in-order traversal of the tree.
defTree.toList (Tree.toList: {β : Type u_1} → Tree β → List (Nat × β)t :t: Tree βTreeTree: Type u_1 → Type u_1β) :β: Type u_1List (List: Type u_1 → Type u_1Nat ×Nat: Typeβ) := matchβ: Type u_1t with |t: Tree βleaf =>leaf: {β : Type ?u.2332} → Tree β[] |[]: List (Nat × β)nodenode: {β : Type ?u.2344} → Tree β → Nat → β → Tree β → Tree βll: Tree βkk: Natvv: βr =>r: Tree βl.l: Tree βtoList ++ [(toList: {β : Type u_1} → Tree β → List (Nat × β)k,k: Natv)] ++v: βr.r: Tree βtoListtoList: {β : Type u_1} → Tree β → List (Nat × β)Tree.leaf.Tree.leaf: {β : Type} → Tree βinsertinsert: {β : Type} → Tree β → Nat → β → Tree β22: Nat"two" |>."two": Stringinsertinsert: {β : Type} → Tree β → Nat → β → Tree β33: Nat"three" |>."three": Stringinsertinsert: {β : Type} → Tree β → Nat → β → Tree β11: Nat"one""one": StringTree.leaf.Tree.leaf: {β : Type} → Tree βinsertinsert: {β : Type} → Tree β → Nat → β → Tree β22: Nat"two" |>."two": Stringinsertinsert: {β : Type} → Tree β → Nat → β → Tree β33: Nat"three" |>."three": Stringinsertinsert: {β : Type} → Tree β → Nat → β → Tree β11: Nat"one" |>."one": StringtoListtoList: {β : Type} → Tree β → List (Nat × β)
The implementation of Tree.toList is inefficient because of how it uses the ++ operator.
On a balanced tree its running time is linearithmic, because it does a linear number of
concatenations at each level of the tree. On an unbalanced tree it's quadratic time.
Here's a tail-recursive implementation than runs in linear time, regardless of whether the tree is balanced:
def Tree.toListTR: {β : Type u_1} → Tree β → List (Nat × β)
Tree.toListTR (t: Tree β
t : Tree: Type u_1 → Type u_1
Tree β: Type u_1
β) : List: Type u_1 → Type u_1
List (Nat: Type
Nat × β: Type u_1
β) :=
go: Tree β → List (Nat × β) → List (Nat × β)
go t: Tree β
t []: List (Nat × β)
[]
where
go: Tree β → List (Nat × β) → List (Nat × β)
go (t: Tree β
t : Tree: Type u_1 → Type u_1
Tree β: Type u_1
β) (acc: List (Nat × β)
acc : List: Type u_1 → Type u_1
List (Nat: Type
Nat × β: Type u_1
β)) : List: Type u_1 → Type u_1
List (Nat: Type
Nat × β: Type u_1
β) :=
match t: Tree β
t with
| leaf: {β : Type ?u.3215} → Tree β
leaf => acc: List (Nat × β)
acc
| node: {β : Type ?u.3225} → Tree β → Nat → β → Tree β → Tree β
node l: Tree β
l k: Nat
k v: β
v r: Tree β
r => go: Tree β → List (Nat × β) → List (Nat × β)
go l: Tree β
l ((k: Nat
k, v: β
v) :: go: Tree β → List (Nat × β) → List (Nat × β)
go r: Tree β
r acc: List (Nat × β)
acc)
We now prove that t.toList and t.toListTR return the same list.
The proof is on induction, and as we used the auxiliary function go
to define Tree.toListTR, we use the auxiliary theorem go to prove the theorem.
The proof of the auxiliary theorem is by induction on t.
The generalizing acc modifier instructs Lean to revert acc, apply the
induction theorem for Trees, and then reintroduce acc in each case.
By using generalizing, we obtain the more general induction hypotheses
-
left_ih : ∀ acc, toListTR.go left acc = toList left ++ acc -
right_ih : ∀ acc, toListTR.go right acc = toList right ++ acc
Recall that the combinator tac <;> tac' runs tac on the main goal and tac' on each produced goal,
concatenating all goals produced by tac'. In this theorem, we use it to apply
simp and close each subgoal produced by the induction tactic.
The simp parameters toListTR.go and toList instruct the simplifier to try to reduce
and/or apply auto generated equation theorems for these two functions.
The parameter * instructs the simplifier to use any equation in a goal as rewriting rules.
In this particular case, simp uses the induction hypotheses as rewriting rules.
Finally, the parameter List.append_assoc instructs the simplifier to use the
List.append_assoc theorem as a rewriting rule.
Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙β: Type u_1
t: Tree β
acc: List (Nat × β)
leaftoListTR.go leaf acc = leaf.toList ++ accβ: Type u_1
t, left✝: Tree β
key✝: Nat
value✝: β
right✝: Tree β
left_ih✝: ∀ (acc : List (Nat × β)), toListTR.go left✝ acc = left✝.toList ++ acc
right_ih✝: ∀ (acc : List (Nat × β)), toListTR.go right✝ acc = right✝.toList ++ acc
acc: List (Nat × β)toListTR.go (left✝.node key✝ value✝ right✝) acc = (left✝.node key✝ value✝ right✝).toList ++ accβ: Type u_1
t: Tree β
acc: List (Nat × β)
leaftoListTR.go leaf acc = leaf.toList ++ accβ: Type u_1
t, left✝: Tree β
key✝: Nat
value✝: β
right✝: Tree β
left_ih✝: ∀ (acc : List (Nat × β)), toListTR.go left✝ acc = left✝.toList ++ acc
right_ih✝: ∀ (acc : List (Nat × β)), toListTR.go right✝ acc = right✝.toList ++ acc
acc: List (Nat × β)toListTR.go (left✝.node key✝ value✝ right✝) acc = (left✝.node key✝ value✝ right✝).toList ++ accGoals accomplished! 🐙
The [csimp] annotation instructs the Lean code generator to replace
any Tree.toList with Tree.toListTR when generating code.
@[csimp]Goals accomplished! 🐙β: Type u_1
t: Tree β
h.ht.toList = t.toListTRGoals accomplished! 🐙
The implementations of Tree.find? and Tree.insert assume that values of type tree obey the BST invariant:
for any non-empty node with key k, all the values of the left subtree are less than k and all the values
of the right subtree are greater than k. But that invariant is not part of the definition of tree.
So, let's formalize the BST invariant. Here's one way to do so. First, we define a helper ForallTree
to express that idea that a predicate holds at every node of a tree:
inductive ForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Prop
ForallTree (p: Nat → β → Prop
p : Nat: Type
Nat → β: Type u_1
β → Prop: Type
Prop) : Tree: Type u_1 → Type u_1
Tree β: Type u_1
β → Prop: Type
Prop
| leaf: ∀ {β : Type u_1} {p : Nat → β → Prop}, ForallTree p Tree.leaf
leaf : ForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Prop
ForallTree p: Nat → β → Prop
p .leaf: {β : Type u_1} → Tree β
.leaf
| node: ∀ {β : Type u_1} {p : Nat → β → Prop} {left : Tree β} {key : Nat} {value : β} {right : Tree β},
ForallTree p left → p key value → ForallTree p right → ForallTree p (left.node key value right)
node :
ForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Prop
ForallTree p: Nat → β → Prop
p left: Tree β
left →
p: Nat → β → Prop
p key: Nat
key value: β
value →
ForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Prop
ForallTree p: Nat → β → Prop
p right: Tree β
right →
ForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Prop
ForallTree p: Nat → β → Prop
p (.node: {β : Type u_1} → Tree β → Nat → β → Tree β → Tree β
.node left: Tree β
left key: Nat
key value: β
value right: Tree β
right)
Second, we define the BST invariant: An empty tree is a BST. A non-empty tree is a BST if all its left nodes have a lesser key, its right nodes have a greater key, and the left and right subtrees are themselves BSTs.
inductiveBST :BST: {β : Type u_1} → Tree β → PropTreeTree: Type u_1 → Type u_1β →β: Type u_1Prop |Prop: Typeleaf :leaf: ∀ {β : Type u_1}, BST Tree.leafBSTBST: {β : Type u_1} → Tree β → Prop.leaf |.leaf: {β : Type u_1} → Tree βnode :node: ∀ {β : Type u_1} {key : Nat} {left right : Tree β} {value : β}, ForallTree (fun k v => k < key) left → ForallTree (fun k v => key < k) right → BST left → BST right → BST (left.node key value right)ForallTree (funForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Propkk: Nat=>k <k: Natkey)key: Natleft →left: Tree ?m.5051ForallTree (funForallTree: {β : Type u_1} → (Nat → β → Prop) → Tree β → Propkk: Nat=>key <key: Natk)k: Natright →right: Tree ?m.5051BSTBST: {β : Type u_1} → Tree β → Propleft →left: Tree ?m.5051BSTBST: {β : Type u_1} → Tree β → Propright →right: Tree ?m.5051BST (BST: {β : Type u_1} → Tree β → Prop.node.node: {β : Type u_1} → Tree β → Nat → β → Tree β → Tree βleftleft: Tree ?m.5051keykey: Natvaluevalue: ?m.5051right)right: Tree ?m.5051
We can use the macro command to create helper tactics for organizing our proofs.
The macro have_eq x y tries to prove x = y using linear arithmetic, and then
immediately uses the new equality to substitute x with y everywhere in the goal.
The modifier local specifies the scope of the macro.
/-- The `have_eq lhs rhs` tactic (tries to) prove that `lhs = rhs`,
and then replaces `lhs` with `rhs`. -/
local macro "have_eq " lhs: Lean.TSyntax `term
lhs:term: Lean.Parser.Category
term:max rhs: Lean.TSyntax `term
rhs:term: Lean.Parser.Category
term:max : tactic: Lean.Parser.Category
tactic =>
`(tactic|
(have h : $lhs: Lean.TSyntax `term
lhs = $rhs: Lean.TSyntax `term
rhs :=
-- TODO: replace with linarith
by simp +arith at *; apply Nat.le_antisymm <;> assumption
try subst $lhs: Lean.TSyntax `term
lhs))
The by_cases' e is just the regular by_cases followed by simp using all
hypotheses in the current goal as rewriting rules.
Recall that the by_cases tactic creates two goals. One where we have h : e and
another one containing h : ¬ e. The simplifier uses the h to rewrite e to True
in the first subgoal, and e to False in the second. This is particularly
useful if e is the condition of an if-statement.
/-- `by_cases' e` is a shorthand form `by_cases e <;> simp[*]` -/
local macro "by_cases' " e: Lean.TSyntax `term
e:term: Lean.Parser.Category
term : tactic: Lean.Parser.Category
tactic =>
`(tactic| by_cases $e: Lean.TSyntax `term
e <;> simp [*])
We can use the attribute [simp] to instruct the simplifier to reduce given definitions or
apply rewrite theorems. The local modifier limits the scope of this modification to this file.
attribute [local simp] Tree.insert: {β : Type u_1} → Tree β → Nat → β → Tree β
Tree.insert
We now prove that Tree.insert preserves the BST invariant using induction and case analysis.
Recall that the tactic . tac focuses on the main goal and tries to solve it using tac, or else fails.
It is used to structure proofs in Lean.
The notation ‹e› is just syntax sugar for (by assumption : e). That is, it tries to find a hypothesis h : e.
It is useful to access hypothesis that have auto generated names (aka "inaccessible") names.
Goals accomplished! 🐙β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₁: ForallTree p t
h₂: p key valueForallTree p (t.insert key value)Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
nodeForallTree p ((left✝.node k value✝ right✝).insert key value)β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝: key < k
posForallTree p ((left✝.insert key value).node k value✝ right✝)β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝: ¬key < kForallTree p (if k < key then left✝.node k value✝ (right✝.insert key value) else left✝.node key value right✝)β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝: key < k
posForallTree p ((left✝.insert key value).node k value✝ right✝)Goals accomplished! 🐙β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝: ¬key < k
negForallTree p (if k < key then left✝.node k value✝ (right✝.insert key value) else left✝.node key value right✝)β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝¹: ¬key < k
h✝: k < key
posForallTree p (left✝.node k value✝ (right✝.insert key value))β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝¹: ¬key < k
h✝: ¬k < keyForallTree p (left✝.node key value right✝)β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝¹: ¬key < k
h✝: k < key
posForallTree p (left✝.node k value✝ (right✝.insert key value))Goals accomplished! 🐙β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
key: Nat
value: β✝
h₂: p key value
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
ihl: ForallTree p (left✝.insert key value)
ihr: ForallTree p (right✝.insert key value)
h✝¹: ¬key < k
h✝: ¬k < key
negForallTree p (left✝.node key value right✝)β✝: Type u_1
p: Nat → β✝ → Prop
t: Tree β✝
value: β✝
left✝: Tree β✝
k: Nat
value✝: β✝
right✝: Tree β✝
hl: ForallTree p left✝
hp: p k value✝
hr: ForallTree p right✝
h₂: p k value
ihl: ForallTree p (left✝.insert k value)
ihr: ForallTree p (right✝.insert k value)
h✝¹, h✝: ¬k < k
negForallTree p (left✝.node k value right✝)Goals accomplished! 🐙Goals accomplished! 🐙β: Type u_1
t: Tree β
h: BST t
key: Nat
value: βBST (t.insert key value)Goals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
nodeBST ((left✝.node k value✝ right✝).insert key value)β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
nodeBST (if key < k then (left✝.insert key value).node k value✝ right✝ else if k < key then left✝.node k value✝ (right✝.insert key value) else left✝.node key value right✝)β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝: key < k
posBST ((left✝.insert key value).node k value✝ right✝)β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝: ¬key < kBST (if k < key then left✝.node k value✝ (right✝.insert key value) else left✝.node key value right✝)β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝: key < k
posBST ((left✝.insert key value).node k value✝ right✝)Goals accomplished! 🐙β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝: ¬key < k
negBST (if k < key then left✝.node k value✝ (right✝.insert key value) else left✝.node key value right✝)β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝¹: ¬key < k
h✝: k < key
posBST (left✝.node k value✝ (right✝.insert key value))β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝¹: ¬key < k
h✝: ¬k < keyBST (left✝.node key value right✝)β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝¹: ¬key < k
h✝: k < key
posBST (left✝.node k value✝ (right✝.insert key value))Goals accomplished! 🐙β: Type u_1
t: Tree β
key: Nat
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert key value)
ih₂: BST (right✝.insert key value)
h✝¹: ¬key < k
h✝: ¬k < key
negBST (left✝.node key value right✝)β: Type u_1
t: Tree β
value: β
k: Nat
left✝, right✝: Tree β
value✝: β
h₁: ForallTree (fun k_1 v => k_1 < k) left✝
h₂: ForallTree (fun k_1 v => k < k_1) right✝
b₁: BST left✝
b₂: BST right✝
ih₁: BST (left✝.insert k value)
ih₂: BST (right✝.insert k value)
h✝¹, h✝: ¬k < k
negBST (left✝.node k value right✝)Goals accomplished! 🐙
Now, we define the type BinTree using a Subtype that states that only trees satisfying the BST invariant are BinTrees.
def BinTree: Type u → Type u
BinTree (β: Type u
β : Type u: Type (u + 1)
Type u) := { t: Tree β
t : Tree: Type u → Type u
Tree β: Type u
β // BST: {β : Type u} → Tree β → Prop
BST t: Tree β
t }
def BinTree.mk: {β : Type u_1} → BinTree β
BinTree.mk : BinTree: Type u_1 → Type u_1
BinTree β: Type u_1
β :=
⟨.leaf: {β : Type u_1} → Tree β
.leaf, .leaf: ∀ {β : Type u_1}, BST Tree.leaf
.leaf⟩
def BinTree.contains: {β : Type u_1} → BinTree β → Nat → Bool
BinTree.contains (b: BinTree β
b : BinTree: Type u_1 → Type u_1
BinTree β: Type u_1
β) (k: Nat
k : Nat: Type
Nat) : Bool: Type
Bool :=
b: BinTree β
b.val: {α : Type u_1} → {p : α → Prop} → Subtype p → α
val.contains: {β : Type u_1} → Tree β → Nat → Bool
contains k: Nat
k
def BinTree.find?: {β : Type u_1} → BinTree β → Nat → Option β
BinTree.find? (b: BinTree β
b : BinTree: Type u_1 → Type u_1
BinTree β: Type u_1
β) (k: Nat
k : Nat: Type
Nat) : Option: Type u_1 → Type u_1
Option β: Type u_1
β :=
b: BinTree β
b.val: {α : Type u_1} → {p : α → Prop} → Subtype p → α
val.find?: {β : Type u_1} → Tree β → Nat → Option β
find? k: Nat
k
def BinTree.insert: {β : Type u_1} → BinTree β → Nat → β → BinTree β
BinTree.insert (b: BinTree β
b : BinTree: Type u_1 → Type u_1
BinTree β: Type u_1
β) (k: Nat
k : Nat: Type
Nat) (v: β
v : β: Type u_1
β) : BinTree: Type u_1 → Type u_1
BinTree β: Type u_1
β :=
⟨b: BinTree β
b.val: {α : Type u_1} → {p : α → Prop} → Subtype p → α
val.insert: {β : Type u_1} → Tree β → Nat → β → Tree β
insert k: Nat
k v: β
v, b: BinTree β
b.val: {α : Type u_1} → {p : α → Prop} → Subtype p → α
val.bst_insert_of_bst: ∀ {β : Type u_1} {t : Tree β}, BST t → ∀ (key : Nat) (value : β), BST (t.insert key value)
bst_insert_of_bst b: BinTree β
b.property: ∀ {α : Type u_1} {p : α → Prop} (self : Subtype p), p self.val
property k: Nat
k v: β
v⟩
Finally, we prove that BinTree.find? and BinTree.insert satisfy the map properties.
attribute [local simp]BinTree.mkBinTree.mk: {β : Type u_1} → BinTree βBinTree.containsBinTree.contains: {β : Type u_1} → BinTree β → Nat → BoolBinTree.find?BinTree.find?: {β : Type u_1} → BinTree β → Nat → Option βBinTree.insertBinTree.insert: {β : Type u_1} → BinTree β → Nat → β → BinTree βTree.find?Tree.find?: {β : Type u_1} → Tree β → Nat → Option βTree.containsTree.contains: {β : Type u_1} → Tree β → Nat → BoolTree.insertTree.insert: {β : Type u_1} → Tree β → Nat → β → Tree βGoals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙;β: Type u_1
b: BinTree β
k: Nat
v: β
t: Tree β
h: BST t(insert ⟨t, h⟩ k v).find? k = some vβ: Type u_1
b: BinTree β
k: Nat
v: β
t: Tree β
h: BST t(t.insert k v).find? k = some vβ: Type u_1
b: BinTree β
k: Nat
v: β
t: Tree β
h: BST t(t.insert k v).find? k = some vβ: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h: BST (left.node key value right)
node(if k < key then (left.insert k v).node key value right else if key < k then left.node key value (right.insert k v) else left.node k v right).find? k = some vGoals accomplished! 🐙β: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h: BST (left.node key value right)
h✝: k < key
pos(left.insert k v).find? k = some vβ: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h: BST (left.node key value right)
h✝: ¬k < key(if key < k then left.node key value (right.insert k v) else left.node k v right).find? k = some vβ: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h: BST (left.node key value right)
h✝: k < key
pos(left.insert k v).find? k = some v;β: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h✝: k < key
a✝³: BST left
a✝²: ForallTree (fun k v => k < key) left
a✝¹: BST right
a✝: ForallTree (fun k v => key < k) right
pos.node(left.insert k v).find? k = some v;β: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h✝: k < key
a✝³: BST left
a✝²: ForallTree (fun k v => k < key) left
a✝¹: BST right
a✝: ForallTree (fun k v => key < k) right
pos.nodeBST leftGoals accomplished! 🐙β: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h: BST (left.node key value right)
h✝: ¬k < key
neg(if key < k then left.node key value (right.insert k v) else left.node k v right).find? k = some vβ: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h: BST (left.node key value right)
h✝¹: ¬k < key
h✝: key < k
pos(right.insert k v).find? k = some v;β: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h✝¹: ¬k < key
h✝: key < k
a✝³: BST left
a✝²: ForallTree (fun k v => k < key) left
a✝¹: BST right
a✝: ForallTree (fun k v => key < k) right
pos.node(right.insert k v).find? k = some v;β: Type u_1
b: BinTree β
k: Nat
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k = some v
ihr: BST right → (right.insert k v).find? k = some v
h✝¹: ¬k < key
h✝: key < k
a✝³: BST left
a✝²: ForallTree (fun k v => k < key) left
a✝¹: BST right
a✝: ForallTree (fun k v => key < k) right
pos.nodeBST rightGoals accomplished! 🐙Goals accomplished! 🐙;β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
t: Tree β
h: BST t(insert ⟨t, h⟩ k v).find? k' = find? ⟨t, h⟩ k'β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
t: Tree β
h: BST t(t.insert k v).find? k' = t.find? k'β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
t: Tree β
h: BST t(t.insert k v).find? k' = t.find? k'β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
h: BST Tree.leaf
leafk ≤ k' → k < k'Goals accomplished! 🐙β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
h: BST Tree.leaf
le: k ≤ k'
leafk < k'Goals accomplished! 🐙Goals accomplished! 🐙β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihl: BST left → (left.insert k v).find? k' = left.find? k'
ihr: BST right → (right.insert k v).find? k' = right.find? k'
h: BST (left.node key value right)
hl: ForallTree (fun k v => k < key) left
hr: ForallTree (fun k v => key < k) right
bl: BST left
br: BST right
node(if k < key then (left.insert k v).node key value right else if key < k then left.node key value (right.insert k v) else left.node k v right).find? k' = if k' < key then left.find? k' else if key < k' then right.find? k' else some valueβ: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
key: Nat
value: β
right: Tree β
ihr: BST right → (right.insert k v).find? k' = right.find? k'
h: BST (left.node key value right)
hl: ForallTree (fun k v => k < key) left
hr: ForallTree (fun k v => key < k) right
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
node(if k < key then (left.insert k v).node key value right else if key < k then left.node key value (right.insert k v) else left.node k v right).find? k' = if k' < key then left.find? k' else if key < k' then right.find? k' else some valueβ: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
key: Nat
value: β
right: Tree β
h: BST (left.node key value right)
hl: ForallTree (fun k v => k < key) left
hr: ForallTree (fun k v => key < k) right
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
ihr: (right.insert k v).find? k' = right.find? k'
node(if k < key then (left.insert k v).node key value right else if key < k then left.node key value (right.insert k v) else left.node k v right).find? k' = if k' < key then left.find? k' else if key < k' then right.find? k' else some value;β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
key: Nat
value: β
right: Tree β
h: BST (left.node key value right)
hl: ForallTree (fun k v => k < key) left
hr: ForallTree (fun k v => key < k) right
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
ihr: (right.insert k v).find? k' = right.find? k'
h✝: ¬k < key
neg(if key < k then left.node key value (right.insert k v) else left.node k v right).find? k' = if k' < key then left.find? k' else if key < k' then right.find? k' else some valueβ: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
key: Nat
value: β
right: Tree β
h: BST (left.node key value right)
hl: ForallTree (fun k v => k < key) left
hr: ForallTree (fun k v => key < k) right
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
ihr: (right.insert k v).find? k' = right.find? k'
h✝¹: ¬k < key
h✝: ¬key < k
neg(if k' < k then left.find? k' else if k < k' then right.find? k' else some v) = if k' < key then left.find? k' else if key < k' then right.find? k' else some valueβ: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
value: β
right: Tree β
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
ihr: (right.insert k v).find? k' = right.find? k'
h: BST (left.node k value right)
hl: ForallTree (fun k_1 v => k_1 < k) left
hr: ForallTree (fun k_1 v => k < k_1) right
h✝¹, h✝: ¬k < k
neg(if k' < k then left.find? k' else if k < k' then right.find? k' else some v) = if k' < k then left.find? k' else if k < k' then right.find? k' else some value;β: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
value: β
right: Tree β
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
ihr: (right.insert k v).find? k' = right.find? k'
h: BST (left.node k value right)
hl: ForallTree (fun k_1 v => k_1 < k) left
hr: ForallTree (fun k_1 v => k < k_1) right
h✝², h✝¹: ¬k < k
h✝: ¬k' < k
neg(if k < k' then right.find? k' else some v) = if k < k' then right.find? k' else some valueβ: Type u_1
k, k': Nat
b: BinTree β
ne: k ≠ k'
v: β
left: Tree β
value: β
right: Tree β
bl: BST left
br: BST right
ihl: (left.insert k v).find? k' = left.find? k'
ihr: (right.insert k v).find? k' = right.find? k'
h: BST (left.node k value right)
hl: ForallTree (fun k_1 v => k_1 < k) left
hr: ForallTree (fun k_1 v => k < k_1) right
h✝³, h✝²: ¬k < k
h✝¹: ¬k' < k
h✝: ¬k < k'
negv = valueβ: Type u_1
k': Nat
b: BinTree β
v: β
left: Tree β
value: β
right: Tree β
bl: BST left
br: BST right
ne: k' ≠ k'
ihl: (left.insert k' v).find? k' = left.find? k'
ihr: (right.insert k' v).find? k' = right.find? k'
h: BST (left.node k' value right)
hl: ForallTree (fun k v => k < k') left
hr: ForallTree (fun k v => k' < k) right
h✝³, h✝², h✝¹, h✝: ¬k' < k'
negv = valueGoals accomplished! 🐙
A Certified Type Checker
In this example, we build a certified type checker for a simple expression language.
Remark: this example is based on an example in the book Certified Programming with Dependent Types by Adam Chlipala.
inductive Expr: Type
Expr where
| nat: Nat → Expr
nat : Nat: Type
Nat → Expr: Type
Expr
| plus: Expr → Expr → Expr
plus : Expr: Type
Expr → Expr: Type
Expr → Expr: Type
Expr
| bool: Bool → Expr
bool : Bool: Type
Bool → Expr: Type
Expr
| and: Expr → Expr → Expr
and : Expr: Type
Expr → Expr: Type
Expr → Expr: Type
Expr
We define a simple language of types using the inductive datatype Ty, and
its typing rules using the inductive predicate HasType.
inductive Ty: Type
Ty where
| nat: Ty
nat
| bool: Ty
bool
deriving DecidableEq: Sort u → Sort (max 1 u)
DecidableEq
inductive HasType: Expr → Ty → Prop
HasType : Expr: Type
Expr → Ty: Type
Ty → Prop: Type
Prop
| nat: ∀ {v : Nat}, HasType (Expr.nat v) Ty.nat
nat : HasType: Expr → Ty → Prop
HasType (.nat: Nat → Expr
.nat v: Nat
v) .nat: Ty
.nat
| plus: ∀ {a b : Expr}, HasType a Ty.nat → HasType b Ty.nat → HasType (a.plus b) Ty.nat
plus : HasType: Expr → Ty → Prop
HasType a: Expr
a .nat: Ty
.nat → HasType: Expr → Ty → Prop
HasType b: Expr
b .nat: Ty
.nat → HasType: Expr → Ty → Prop
HasType (.plus: Expr → Expr → Expr
.plus a: Expr
a b: Expr
b) .nat: Ty
.nat
| bool: ∀ {v : Bool}, HasType (Expr.bool v) Ty.bool
bool : HasType: Expr → Ty → Prop
HasType (.bool: Bool → Expr
.bool v: Bool
v) .bool: Ty
.bool
| and: ∀ {a b : Expr}, HasType a Ty.bool → HasType b Ty.bool → HasType (a.and b) Ty.bool
and : HasType: Expr → Ty → Prop
HasType a: Expr
a .bool: Ty
.bool → HasType: Expr → Ty → Prop
HasType b: Expr
b .bool: Ty
.bool → HasType: Expr → Ty → Prop
HasType (.and: Expr → Expr → Expr
.and a: Expr
a b: Expr
b) .bool: Ty
.bool
We can easily show that if e has type t₁ and type t₂, then t₁ and t₂ must be equal
by using the cases tactic. This tactic creates a new subgoal for every constructor,
and automatically discharges unreachable cases. The tactic combinator tac₁ <;> tac₂ applies
tac₂ to each subgoal produced by tac₁. Then, the tactic rfl is used to close all produced
goals using reflexivity.
Goals accomplished! 🐙t₂: Ty
v✝: Nat
h₂: HasType (Expr.nat v✝) t₂
natTy.nat = t₂t₂: Ty
a✝², b✝: Expr
a✝¹: HasType a✝² Ty.nat
a✝: HasType b✝ Ty.nat
h₂: HasType (a✝².plus b✝) t₂Ty.nat = t₂t₂: Ty
v✝: Bool
h₂: HasType (Expr.bool v✝) t₂Ty.bool = t₂t₂: Ty
a✝², b✝: Expr
a✝¹: HasType a✝² Ty.bool
a✝: HasType b✝ Ty.bool
h₂: HasType (a✝².and b✝) t₂Ty.bool = t₂t₂: Ty
v✝: Nat
h₂: HasType (Expr.nat v✝) t₂
natTy.nat = t₂t₂: Ty
a✝², b✝: Expr
a✝¹: HasType a✝² Ty.nat
a✝: HasType b✝ Ty.nat
h₂: HasType (a✝².plus b✝) t₂Ty.nat = t₂t₂: Ty
v✝: Bool
h₂: HasType (Expr.bool v✝) t₂Ty.bool = t₂t₂: Ty
a✝², b✝: Expr
a✝¹: HasType a✝² Ty.bool
a✝: HasType b✝ Ty.bool
h₂: HasType (a✝².and b✝) t₂Ty.bool = t₂a✝⁴, b✝: Expr
a✝³: HasType a✝⁴ Ty.nat
a✝²: HasType b✝ Ty.nat
a✝¹: HasType a✝⁴ Ty.nat
a✝: HasType b✝ Ty.nat
plus.plusTy.nat = Ty.natv✝: Nat
nat.natTy.nat = Ty.nata✝⁴, b✝: Expr
a✝³: HasType a✝⁴ Ty.nat
a✝²: HasType b✝ Ty.nat
a✝¹: HasType a✝⁴ Ty.nat
a✝: HasType b✝ Ty.natTy.nat = Ty.natv✝: BoolTy.bool = Ty.boola✝⁴, b✝: Expr
a✝³: HasType a✝⁴ Ty.bool
a✝²: HasType b✝ Ty.bool
a✝¹: HasType a✝⁴ Ty.bool
a✝: HasType b✝ Ty.boolTy.bool = Ty.boolGoals accomplished! 🐙
The inductive type Maybe p has two constructors: found a h and unknown.
The former contains an element a : α and a proof that a satisfies the predicate p.
The constructor unknown is used to encode "failure".
inductive Maybe: {α : Sort u_1} → (α → Prop) → Sort (max 1 u_1)
Maybe (p: α → Prop
p : α: Sort u_1
α → Prop: Type
Prop) where
| found: {α : Sort u_1} → {p : α → Prop} → (a : α) → p a → Maybe p
found : (a: α
a : α: Sort u_1
α) → p: α → Prop
p a: α
a → Maybe: {α : Sort u_1} → (α → Prop) → Sort (max 1 u_1)
Maybe p: α → Prop
p
| unknown: {α : Sort u_1} → {p : α → Prop} → Maybe p
unknown
We define a notation for Maybe that is similar to the builtin notation for the Lean builtin type Subtype.
notation "{{ " x: Lean.TSyntax `term
x " | " p: Lean.TSyntax `term
p " }}" => Maybe: {α : Sort u_1} → (α → Prop) → Sort (max 1 u_1)
Maybe (fun x: Lean.TSyntax `term
x => p: Lean.TSyntax `term
p)
The function Expr.typeCheck e returns a type ty and a proof that e has type ty,
or unknown.
Recall that, def Expr.typeCheck ... in Lean is notation for namespace Expr def typeCheck ... end Expr.
The term .found .nat .nat is sugar for Maybe.found Ty.nat HasType.nat. Lean can infer the namespaces using
the expected types.
defExpr.typeCheck (Expr.typeCheck: (e : Expr) → {{ ty | HasType e ty }}e :e: ExprExpr) : {{Expr: Typety |ty: TyHasTypeHasType: Expr → Ty → Propee: Exprty }} := matchty: Tye with |e: Exprnat .. =>nat: Nat → Expr.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.nat.nat: Ty.nat |.nat: ∀ {v : Nat}, HasType (nat v) Ty.natbool .. =>bool: Bool → Expr.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.bool.bool: Ty.bool |.bool: ∀ {v : Bool}, HasType (bool v) Ty.boolplusplus: Expr → Expr → Expraa: Exprb => matchb: Expra.a: ExprtypeCheck,typeCheck: (e : Expr) → {{ ty | HasType e ty }}b.b: ExprtypeCheck with |typeCheck: (e : Expr) → {{ ty | HasType e ty }}.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.nat.nat: Tyh₁,h₁: HasType a Ty.nat.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.nat.nat: Tyh₂ =>h₂: HasType b Ty.nat.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.nat (.nat: Ty.plus.plus: ∀ {a b : Expr}, HasType a Ty.nat → HasType b Ty.nat → HasType (a.plus b) Ty.nath₁h₁: HasType a Ty.nath₂) | _, _ =>h₂: HasType b Ty.nat.unknown |.unknown: {α : Type} → {p : α → Prop} → Maybe pandand: Expr → Expr → Expraa: Exprb => matchb: Expra.a: ExprtypeCheck,typeCheck: (e : Expr) → {{ ty | HasType e ty }}b.b: ExprtypeCheck with |typeCheck: (e : Expr) → {{ ty | HasType e ty }}.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.bool.bool: Tyh₁,h₁: HasType a Ty.bool.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.bool.bool: Tyh₂ =>h₂: HasType b Ty.bool.found.found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p.bool (.bool: Ty.and.and: ∀ {a b : Expr}, HasType a Ty.bool → HasType b Ty.bool → HasType (a.and b) Ty.boolh₁h₁: HasType a Ty.boolh₂) | _, _ =>h₂: HasType b Ty.bool.unknown.unknown: {α : Type} → {p : α → Prop} → Maybe pGoals accomplished! 🐙e: Expr
ty: Ty
h, h₁: HasType e tye.typeCheck ≠ Maybe.unknown → e.typeCheck = Maybe.found ty he: Expr
ty: Ty
h, h₁: HasType e ty
x✝: {{ ty | HasType e ty }}x✝ ≠ Maybe.unknown → x✝ = Maybe.found ty hGoals accomplished! 🐙;e: Expr
ty: Ty
h, h₁: HasType e ty
ty': Ty
h': HasType e ty'
h₂✝: Maybe.found ty' h' ≠ Maybe.unknown
foundMaybe.found ty' h' = Maybe.found ty h;e: Expr
ty: Ty
h, h₁: HasType e ty
ty': Ty
h': HasType e ty'
h₂✝: Maybe.found ty' h' ≠ Maybe.unknown
this: ty = ty'
foundMaybe.found ty' h' = Maybe.found ty h;e: Expr
ty: Ty
h, h₁, h': HasType e ty
h₂✝: Maybe.found ty h' ≠ Maybe.unknown
foundMaybe.found ty h' = Maybe.found ty hGoals accomplished! 🐙Goals accomplished! 🐙;e: Expr
ty: Ty
h, h₁: HasType e ty
h₂✝: Maybe.unknown ≠ Maybe.unknown
unknownMaybe.unknown = Maybe.found ty hGoals accomplished! 🐙
Now, we prove that if Expr.typeCheck e returns Maybe.unknown, then forall ty, HasType e ty does not hold.
The notation e.typeCheck is sugar for Expr.typeCheck e. Lean can infer this because we explicitly said that e has type Expr.
The proof is by induction on e and case analysis. Note that the tactic simp [typeCheck] is applied to all goal generated by the induction tactic, and closes
the cases corresponding to the constructors Expr.nat and Expr.bool.
Goals accomplished! 🐙ty: Ty
e: Expre.typeCheck = Maybe.unknown → ¬HasType e tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
plus(match a.typeCheck, b.typeCheck with | Maybe.found Ty.nat h₁, Maybe.found Ty.nat h₂ => Maybe.found Ty.nat ⋯ | x, x_1 => Maybe.unknown) = Maybe.unknown → ¬HasType (a.plus b) tyGoals accomplished! 🐙ty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝¹: {{ ty | HasType a ty }}
x✝: {{ ty | HasType b ty }}
h₁✝: HasType a Ty.nat
h₂✝: HasType b Ty.nat
heq✝¹: a.typeCheck = Maybe.found Ty.nat h₁✝
heq✝: b.typeCheck = Maybe.found Ty.nat h₂✝
plus.h_1Maybe.found Ty.nat ⋯ = Maybe.unknown → ¬HasType (a.plus b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝²: {{ ty | HasType a ty }}
x✝¹: {{ ty | HasType b ty }}
x✝: ∀ (h₁ : HasType a Ty.nat) (h₂ : HasType b Ty.nat), a.typeCheck = Maybe.found Ty.nat h₁ → b.typeCheck = Maybe.found Ty.nat h₂ → FalseMaybe.unknown = Maybe.unknown → ¬HasType (a.plus b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝¹: {{ ty | HasType a ty }}
x✝: {{ ty | HasType b ty }}
h₁✝: HasType a Ty.nat
h₂✝: HasType b Ty.nat
heq✝¹: a.typeCheck = Maybe.found Ty.nat h₁✝
heq✝: b.typeCheck = Maybe.found Ty.nat h₂✝
plus.h_1Maybe.found Ty.nat ⋯ = Maybe.unknown → ¬HasType (a.plus b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝²: {{ ty | HasType a ty }}
x✝¹: {{ ty | HasType b ty }}
x✝: ∀ (h₁ : HasType a Ty.nat) (h₂ : HasType b Ty.nat), a.typeCheck = Maybe.found Ty.nat h₁ → b.typeCheck = Maybe.found Ty.nat h₂ → FalseMaybe.unknown = Maybe.unknown → ¬HasType (a.plus b) ty;ty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝¹: {{ ty | HasType a ty }}
x✝: {{ ty | HasType b ty }}
h₁✝: HasType a Ty.nat
h₂✝: HasType b Ty.nat
heq✝¹: a.typeCheck = Maybe.found Ty.nat h₁✝
heq✝: b.typeCheck = Maybe.found Ty.nat h₂✝
a✝: Maybe.found Ty.nat ⋯ = Maybe.unknown¬HasType (a.plus b) tyGoals accomplished! 🐙ty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝²: {{ ty | HasType a ty }}
x✝¹: {{ ty | HasType b ty }}
x✝: ∀ (h₁ : HasType a Ty.nat) (h₂ : HasType b Ty.nat), a.typeCheck = Maybe.found Ty.nat h₁ → b.typeCheck = Maybe.found Ty.nat h₂ → False
plus.h_2Maybe.unknown = Maybe.unknown → ¬HasType (a.plus b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
ra: {{ ty | HasType a ty }}
rb: {{ ty | HasType b ty }}
hnp: ∀ (h₁ : HasType a Ty.nat) (h₂ : HasType b Ty.nat), a.typeCheck = Maybe.found Ty.nat h₁ → b.typeCheck = Maybe.found Ty.nat h₂ → False
h: Maybe.unknown = Maybe.unknown
ht: HasType (a.plus b) tyFalsety: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
ra: {{ ty | HasType a ty }}
rb: {{ ty | HasType b ty }}
hnp: ∀ (h₁ : HasType a Ty.nat) (h₂ : HasType b Ty.nat), a.typeCheck = Maybe.found Ty.nat h₁ → b.typeCheck = Maybe.found Ty.nat h₂ → False
h: Maybe.unknown = Maybe.unknown
ht: HasType (a.plus b) tyFalseGoals accomplished! 🐙Goals accomplished! 🐙Goals accomplished! 🐙ty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝¹: {{ ty | HasType a ty }}
x✝: {{ ty | HasType b ty }}
h₁✝: HasType a Ty.bool
h₂✝: HasType b Ty.bool
heq✝¹: a.typeCheck = Maybe.found Ty.bool h₁✝
heq✝: b.typeCheck = Maybe.found Ty.bool h₂✝
and.h_1Maybe.found Ty.bool ⋯ = Maybe.unknown → ¬HasType (a.and b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝²: {{ ty | HasType a ty }}
x✝¹: {{ ty | HasType b ty }}
x✝: ∀ (h₁ : HasType a Ty.bool) (h₂ : HasType b Ty.bool), a.typeCheck = Maybe.found Ty.bool h₁ → b.typeCheck = Maybe.found Ty.bool h₂ → FalseMaybe.unknown = Maybe.unknown → ¬HasType (a.and b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝¹: {{ ty | HasType a ty }}
x✝: {{ ty | HasType b ty }}
h₁✝: HasType a Ty.bool
h₂✝: HasType b Ty.bool
heq✝¹: a.typeCheck = Maybe.found Ty.bool h₁✝
heq✝: b.typeCheck = Maybe.found Ty.bool h₂✝
and.h_1Maybe.found Ty.bool ⋯ = Maybe.unknown → ¬HasType (a.and b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝²: {{ ty | HasType a ty }}
x✝¹: {{ ty | HasType b ty }}
x✝: ∀ (h₁ : HasType a Ty.bool) (h₂ : HasType b Ty.bool), a.typeCheck = Maybe.found Ty.bool h₁ → b.typeCheck = Maybe.found Ty.bool h₂ → FalseMaybe.unknown = Maybe.unknown → ¬HasType (a.and b) ty;ty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝¹: {{ ty | HasType a ty }}
x✝: {{ ty | HasType b ty }}
h₁✝: HasType a Ty.bool
h₂✝: HasType b Ty.bool
heq✝¹: a.typeCheck = Maybe.found Ty.bool h₁✝
heq✝: b.typeCheck = Maybe.found Ty.bool h₂✝
a✝: Maybe.found Ty.bool ⋯ = Maybe.unknown¬HasType (a.and b) tyGoals accomplished! 🐙ty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
x✝²: {{ ty | HasType a ty }}
x✝¹: {{ ty | HasType b ty }}
x✝: ∀ (h₁ : HasType a Ty.bool) (h₂ : HasType b Ty.bool), a.typeCheck = Maybe.found Ty.bool h₁ → b.typeCheck = Maybe.found Ty.bool h₂ → False
and.h_2Maybe.unknown = Maybe.unknown → ¬HasType (a.and b) tyty: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
ra: {{ ty | HasType a ty }}
rb: {{ ty | HasType b ty }}
hnp: ∀ (h₁ : HasType a Ty.bool) (h₂ : HasType b Ty.bool), a.typeCheck = Maybe.found Ty.bool h₁ → b.typeCheck = Maybe.found Ty.bool h₂ → False
h: Maybe.unknown = Maybe.unknown
ht: HasType (a.and b) tyFalsety: Ty
a, b: Expr
iha: a.typeCheck = Maybe.unknown → ¬HasType a ty
ihb: b.typeCheck = Maybe.unknown → ¬HasType b ty
ra: {{ ty | HasType a ty }}
rb: {{ ty | HasType b ty }}
hnp: ∀ (h₁ : HasType a Ty.bool) (h₂ : HasType b Ty.bool), a.typeCheck = Maybe.found Ty.bool h₁ → b.typeCheck = Maybe.found Ty.bool h₂ → False
h: Maybe.unknown = Maybe.unknown
ht: HasType (a.and b) tyFalseGoals accomplished! 🐙Goals accomplished! 🐙
Finally, we show that type checking for e can be decided using Expr.typeCheck.
instance: (e : Expr) → (t : Ty) → Decidable (HasType e t)
instance (e: Expr
e : Expr: Type
Expr) (t: Ty
t : Ty: Type
Ty) : Decidable: Prop → Type
Decidable (HasType: Expr → Ty → Prop
HasType e: Expr
e t: Ty
t) :=
match h': e.typeCheck = Maybe.unknown
h' : e: Expr
e.typeCheck: (e : Expr) → {{ ty | HasType e ty }}
typeCheck with
| .found: {α : Type} → {p : α → Prop} → (a : α) → p a → Maybe p
.found t': Ty
t' ht': HasType e t'
ht' =>
if heq: ¬t = t'
heq : t: Ty
t = t': Ty
t' then
isTrue: {p : Prop} → p → Decidable p
isTrue (heq: t = t'
heq ▸ ht': HasType e t'
ht')
else
isFalse: {p : Prop} → ¬p → Decidable p
isFalse fun ht: HasType e t
ht => heq: ¬t = t'
heq (HasType.det: ∀ {e : Expr} {t₁ t₂ : Ty}, HasType e t₁ → HasType e t₂ → t₁ = t₂
HasType.det ht: HasType e t
ht ht': HasType e t'
ht')
| .unknown: {{ ty | HasType e ty }}
.unknown => isFalse: {p : Prop} → ¬p → Decidable p
isFalse (Expr.typeCheck_complete: ∀ {ty : Ty} {e : Expr}, e.typeCheck = Maybe.unknown → ¬HasType e ty
Expr.typeCheck_complete h': e.typeCheck = Maybe.unknown
h')The Well-Typed Interpreter
In this example, we build an interpreter for a simple functional programming language,
with variables, function application, binary operators and an if...then...else construct.
We will use the dependent type system to ensure that any programs which can be represented are well-typed.
Remark: this example is based on an example found in the Idris manual.
Vectors
A Vec is a list of size n whose elements belong to a type α.
inductive Vec: Type u → Nat → Type u
Vec (α: Type u
α : Type u: Type (u + 1)
Type u) : Nat: Type
Nat → Type u: Type (u + 1)
Type u
| nil: {α : Type u} → Vec α 0
nil : Vec: Type u → Nat → Type u
Vec α: Type u
α 0: Nat
0
| cons: {α : Type u} → {n : Nat} → α → Vec α n → Vec α (n + 1)
cons : α: Type u
α → Vec: Type u → Nat → Type u
Vec α: Type u
α n: Nat
n → Vec: Type u → Nat → Type u
Vec α: Type u
α (n: Nat
n+1: Nat
1)
We can overload the List.cons notation :: and use it to create Vecs.
infix:67 " :: " => Vec.cons: {α : Type u} → {n : Nat} → α → Vec α n → Vec α (n + 1)
Vec.cons
Now, we define the types of our simple functional language.
We have integers, booleans, and functions, represented by Ty.
inductive Ty: Type
Ty where
| int: Ty
int
| bool: Ty
bool
| fn: Ty → Ty → Ty
fn (a: Ty
a r: Ty
r : Ty: Type
Ty)
We can write a function to translate Ty values to a Lean type
— remember that types are first class, so can be calculated just like any other value.
We mark Ty.interp as [reducible] to make sure the typeclass resolution procedure can
unfold/reduce it. For example, suppose Lean is trying to synthesize a value for the instance
Add (Ty.interp Ty.int). Since Ty.interp is marked as [reducible],
the typeclass resolution procedure can reduce Ty.interp Ty.int to Int, and use
the builtin instance for Add Int as the solution.
@[reducible] def Ty.interp: Ty → Type
Ty.interp : Ty: Type
Ty → Type: Type 1
Type
| int: Ty
int => Int: Type
Int
| bool: Ty
bool => Bool: Type
Bool
| fn: Ty → Ty → Ty
fn a: Ty
a r: Ty
r => a: Ty
a.interp: Ty → Type
interp → r: Ty
r.interp: Ty → Type
interp
Expressions are indexed by the types of the local variables, and the type of the expression itself.
inductive HasType: {n : Nat} → Fin n → Vec Ty n → Ty → Type
HasType : Fin: Nat → Type
Fin n: Nat
n → Vec: Type → Nat → Type
Vec Ty: Type
Ty n: Nat
n → Ty: Type
Ty → Type: Type 1
Type where
| stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) ty
stop : HasType: {n : Nat} → Fin n → Vec Ty n → Ty → Type
HasType 0: Fin (?m.2915 + 1)
0 (ty: Ty
ty :: ctx: Vec Ty ?m.2915
ctx) ty: Ty
ty
| pop: {x : Nat} → {k : Fin x} → {ctx : Vec Ty x} → {ty u : Ty} → HasType k ctx ty → HasType k.succ (u :: ctx) ty
pop : HasType: {n : Nat} → Fin n → Vec Ty n → Ty → Type
HasType k: Fin ?m.3128
k ctx: Vec Ty ?m.3128
ctx ty: Ty
ty → HasType: {n : Nat} → Fin n → Vec Ty n → Ty → Type
HasType k: Fin ?m.3128
k.succ: {n : Nat} → Fin n → Fin (n + 1)
succ (u: Ty
u :: ctx: Vec Ty ?m.3128
ctx) ty: Ty
ty
inductive Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr : Vec: Type → Nat → Type
Vec Ty: Type
Ty n: Nat
n → Ty: Type
Ty → Type: Type 1
Type where
| var: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx ty
var : HasType: {n : Nat} → Fin n → Vec Ty n → Ty → Type
HasType i: Fin ?m.4043
i ctx: Vec Ty ?m.4043
ctx ty: Ty
ty → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4043
ctx ty: Ty
ty
| val: {n : Nat} → {ctx : Vec Ty n} → Int → Expr ctx Ty.int
val : Int: Type
Int → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4064
ctx Ty.int: Ty
Ty.int
| lam: {n : Nat} → {a : Ty} → {ctx : Vec Ty n} → {ty : Ty} → Expr (a :: ctx) ty → Expr ctx (a.fn ty)
lam : Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr (a: Ty
a :: ctx: Vec Ty ?m.4238
ctx) ty: Ty
ty → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4238
ctx (Ty.fn: Ty → Ty → Ty
Ty.fn a: Ty
a ty: Ty
ty)
| app: {n : Nat} → {ctx : Vec Ty n} → {a ty : Ty} → Expr ctx (a.fn ty) → Expr ctx a → Expr ctx ty
app : Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4399
ctx (Ty.fn: Ty → Ty → Ty
Ty.fn a: Ty
a ty: Ty
ty) → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4399
ctx a: Ty
a → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4399
ctx ty: Ty
ty
| op: {n : Nat} → {ctx : Vec Ty n} → {a b c : Ty} → (a.interp → b.interp → c.interp) → Expr ctx a → Expr ctx b → Expr ctx c
op : (a: Ty
a.interp: Ty → Type
interp → b: Ty
b.interp: Ty → Type
interp → c: Ty
c.interp: Ty → Type
interp) → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4498
ctx a: Ty
a → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4498
ctx b: Ty
b → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4498
ctx c: Ty
c
| ife: {n : Nat} → {ctx : Vec Ty n} → {a : Ty} → Expr ctx Ty.bool → Expr ctx a → Expr ctx a → Expr ctx a
ife : Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4619
ctx Ty.bool: Ty
Ty.bool → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4619
ctx a: Ty
a → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4619
ctx a: Ty
a → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4619
ctx a: Ty
a
| delay: {n : Nat} → {ctx : Vec Ty n} → {a : Ty} → (Unit → Expr ctx a) → Expr ctx a
delay : (Unit: Type
Unit → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4662
ctx a: Ty
a) → Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.4662
ctx a: Ty
a
We use the command open to create the aliases stop and pop for HasType.stop and HasType.pop respectively.
open HasType (stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) ty
stop pop: {x : Nat} → {k : Fin x} → {ctx : Vec Ty x} → {ty u : Ty} → HasType k ctx ty → HasType k.succ (u :: ctx) ty
pop)
Since expressions are indexed by their type, we can read the typing rules of the language from the definitions of the constructors. Let us look at each constructor in turn.
We use a nameless representation for variables — they are de Bruijn indexed.
Variables are represented by a proof of their membership in the context, HasType i ctx ty,
which is a proof that variable i in context ctx has type ty.
We can treat stop as a proof that the most recently defined variable is well-typed,
and pop n as a proof that, if the nth most recently defined variable is well-typed, so is the n+1th.
In practice, this means we use stop to refer to the most recently defined variable,
pop stop to refer to the next, and so on, via the Expr.var constructor.
A value Expr.val carries a concrete representation of an integer.
A lambda Expr.lam creates a function. In the scope of a function of type Ty.fn a ty, there is a
new local variable of type a.
A function application Expr.app produces a value of type ty given a function from a to ty and a value of type a.
The constructor Expr.op allows us to use arbitrary binary operators, where the type of the operator informs what the types of the arguments must be.
Finally, the constructor Exp.ife represents a if-then-else expression. The condition is a Boolean, and each branch must have the same type.
The auxiliary constructor Expr.delay is used to delay evaluation.
When we evaluate an Expr, we’ll need to know the values in scope, as well as their types. Env is an environment,
indexed over the types in scope. Since an environment is just another form of list, albeit with a strongly specified connection
to the vector of local variable types, we overload again the notation :: so that we can use the usual list syntax.
Given a proof that a variable is defined in the context, we can then produce a value from the environment.
inductive Env: {n : Nat} → Vec Ty n → Type
Env : Vec: Type → Nat → Type
Vec Ty: Type
Ty n: Nat
n → Type: Type 1
Type where
| nil: Env Vec.nil
nil : Env: {n : Nat} → Vec Ty n → Type
Env Vec.nil: {α : Type} → Vec α 0
Vec.nil
| cons: {a : Ty} → {x : Nat} → {ctx : Vec Ty x} → a.interp → Env ctx → Env (a :: ctx)
cons : Ty.interp: Ty → Type
Ty.interp a: Ty
a → Env: {n : Nat} → Vec Ty n → Type
Env ctx: Vec Ty ?m.9565
ctx → Env: {n : Nat} → Vec Ty n → Type
Env (a: Ty
a :: ctx: Vec Ty ?m.9565
ctx)
infix:67 " :: " => Env.cons: {a : Ty} → {x : Nat} → {ctx : Vec Ty x} → a.interp → Env ctx → Env (a :: ctx)
Env.cons
def Env.lookup: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Env ctx → ty.interp
Env.lookup : HasType: {n : Nat} → Fin n → Vec Ty n → Ty → Type
HasType i: Fin ?m.12248
i ctx: Vec Ty ?m.12248
ctx ty: Ty
ty → Env: {n : Nat} → Vec Ty n → Type
Env ctx: Vec Ty ?m.12248
ctx → ty: Ty
ty.interp: Ty → Type
interp
| stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) ty
stop, x: ty.interp
x :: xs: Env ctx✝
xs => x: ty.interp
x
| pop: {x : Nat} → {k : Fin x} → {ctx : Vec Ty x} → {ty u : Ty} → HasType k ctx ty → HasType k.succ (u :: ctx) ty
pop k: HasType k✝ ctx✝ ty
k, x: u✝.interp
x :: xs: Env ctx✝
xs => lookup: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Env ctx → ty.interp
lookup k: HasType k✝ ctx✝ ty
k xs: Env ctx✝
xs
Given this, an interpreter is a function which translates an Expr into a Lean value with respect to a specific environment.
def Expr.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
Expr.interp (env: Env ctx
env : Env: {n : Nat} → Vec Ty n → Type
Env ctx: Vec Ty ?m.15201
ctx) : Expr: {n : Nat} → Vec Ty n → Ty → Type
Expr ctx: Vec Ty ?m.15201
ctx ty: Ty
ty → ty: Ty
ty.interp: Ty → Type
interp
| var: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx ty
var i: HasType i✝ ctx ty
i => env: Env ctx
env.lookup: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Env ctx → ty.interp
lookup i: HasType i✝ ctx ty
i
| val: {n : Nat} → {ctx : Vec Ty n} → Int → Expr ctx Ty.int
val x: Int
x => x: Int
x
| lam: {n : Nat} → {a : Ty} → {ctx : Vec Ty n} → {ty : Ty} → Expr (a :: ctx) ty → Expr ctx (a.fn ty)
lam b: Expr (a✝ :: ctx) ty✝
b => fun x: a✝.interp
x => b: Expr (a✝ :: ctx) ty✝
b.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp (Env.cons: {a : Ty} → {x : Nat} → {ctx : Vec Ty x} → a.interp → Env ctx → Env (a :: ctx)
Env.cons x: a✝.interp
x env: Env ctx
env)
| app: {n : Nat} → {ctx : Vec Ty n} → {a ty : Ty} → Expr ctx (a.fn ty) → Expr ctx a → Expr ctx ty
app f: Expr ctx (a✝.fn ty)
f a: Expr ctx a✝
a => f: Expr ctx (a✝.fn ty)
f.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env (a: Expr ctx a✝
a.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env)
| op: {n : Nat} → {ctx : Vec Ty n} → {a b c : Ty} → (a.interp → b.interp → c.interp) → Expr ctx a → Expr ctx b → Expr ctx c
op o: a✝.interp → b✝.interp → ty.interp
o x: Expr ctx a✝
x y: Expr ctx b✝
y => o: a✝.interp → b✝.interp → ty.interp
o (x: Expr ctx a✝
x.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env) (y: Expr ctx b✝
y.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env)
| ife: {n : Nat} → {ctx : Vec Ty n} → {a : Ty} → Expr ctx Ty.bool → Expr ctx a → Expr ctx a → Expr ctx a
ife c: Expr ctx Ty.bool
c t: Expr ctx ty
t e: Expr ctx ty
e => if c: Expr ctx Ty.bool
c.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env then t: Expr ctx ty
t.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env else e: Expr ctx ty
e.interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env
| delay: {n : Nat} → {ctx : Vec Ty n} → {a : Ty} → (Unit → Expr ctx a) → Expr ctx a
delay a: Unit → Expr ctx ty
a => (a: Unit → Expr ctx ty
a (): Unit
()).interp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interp
interp env: Env ctx
env
open Expr
We can make some simple test functions. Firstly, adding two inputs fun x y => y + x is written as follows.
defadd :add: {a : Nat} → {ctx : Vec Ty a} → Expr ctx (Ty.int.fn (Ty.int.fn Ty.int))ExprExpr: {n : Nat} → Vec Ty n → Ty → Typectx (ctx: Vec Ty ?m.19264Ty.fnTy.fn: Ty → Ty → TyTy.int (Ty.int: TyTy.fnTy.fn: Ty → Ty → TyTy.intTy.int: TyTy.int)) :=Ty.int: Tylam (lam: {n : Nat} → {a : Ty} → {ctx : Vec Ty n} → {ty : Ty} → Expr (a :: ctx) ty → Expr ctx (a.fn ty)lam (lam: {n : Nat} → {a : Ty} → {ctx : Vec Ty n} → {ty : Ty} → Expr (a :: ctx) ty → Expr ctx (a.fn ty)opop: {n : Nat} → {ctx : Vec Ty n} → {a b c : Ty} → (a.interp → b.interp → c.interp) → Expr ctx a → Expr ctx b → Expr ctx c(·+·) ((·+·): Ty.int.interp → Ty.int.interp → Ty.int.interpvarvar: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx tystop) (stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) tyvar (var: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx typoppop: {x : Nat} → {k : Fin x} → {ctx : Vec Ty x} → {ty u : Ty} → HasType k ctx ty → HasType k.succ (u :: ctx) tystop))))stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) tyadd.add: {a : Nat} → {ctx : Vec Ty a} → Expr ctx (Ty.int.fn (Ty.int.fn Ty.int))interpinterp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interpEnv.nilEnv.nil: Env Vec.nil1010: Ty.int.interp2020: Ty.int.interp
More interestingly, a factorial function fact (e.g. fun x => if (x == 0) then 1 else (fact (x-1) * x)), can be written as.
Note that this is a recursive (non-terminating) definition. For every input value, the interpreter terminates, but the
definition itself is non-terminating. We use two tricks to make sure Lean accepts it. First, we use the auxiliary constructor
Expr.delay to delay its unfolding. Second, we add the annotation decreasing_by sorry which can be viewed as
"trust me, this recursive definition makes sense". Recall that sorry is an unsound axiom in Lean.
def:ExprExpr: {n : Nat} → Vec Ty n → Ty → Typectx (ctx: Vec Ty ?m.19660Ty.fnTy.fn: Ty → Ty → TyTy.intTy.int: TyTy.int) :=Ty.int: Tylam (lam: {n : Nat} → {a : Ty} → {ctx : Vec Ty n} → {ty : Ty} → Expr (a :: ctx) ty → Expr ctx (a.fn ty)ife (ife: {n : Nat} → {ctx : Vec Ty n} → {a : Ty} → Expr ctx Ty.bool → Expr ctx a → Expr ctx a → Expr ctx aopop: {n : Nat} → {ctx : Vec Ty n} → {a b c : Ty} → (a.interp → b.interp → c.interp) → Expr ctx a → Expr ctx b → Expr ctx c(·==·) ((·==·): Ty.int.interp → Ty.int.interp → Boolvarvar: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx tystop) (stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) tyvalval: {n : Nat} → {ctx : Vec Ty n} → Int → Expr ctx Ty.int0)) (0: Intvalval: {n : Nat} → {ctx : Vec Ty n} → Int → Expr ctx Ty.int1) (1: Intopop: {n : Nat} → {ctx : Vec Ty n} → {a b c : Ty} → (a.interp → b.interp → c.interp) → Expr ctx a → Expr ctx b → Expr ctx c(·*·) ((·*·): Ty.int.interp → Ty.int.interp → Ty.int.interpdelay fundelay: {n : Nat} → {ctx : Vec Ty n} → {a : Ty} → (Unit → Expr ctx a) → Expr ctx a_ =>_: Unitappapp: {n : Nat} → {ctx : Vec Ty n} → {a ty : Ty} → Expr ctx (a.fn ty) → Expr ctx a → Expr ctx tyfact (fact: {a : Nat} → {ctx : Vec Ty a} → Expr ctx (Ty.int.fn Ty.int)opop: {n : Nat} → {ctx : Vec Ty n} → {a b c : Ty} → (a.interp → b.interp → c.interp) → Expr ctx a → Expr ctx b → Expr ctx c(·-·) ((·-·): Ty.int.interp → Ty.int.interp → Ty.int.interpvarvar: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx tystop) (stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) tyvalval: {n : Nat} → {ctx : Vec Ty n} → Int → Expr ctx Ty.int1))) (1: Intvarvar: {n : Nat} → {i : Fin n} → {ctx : Vec Ty n} → {ty : Ty} → HasType i ctx ty → Expr ctx tystop)))stop: {ty : Ty} → {x : Nat} → {ctx : Vec Ty x} → HasType 0 (ty :: ctx) tya✝: Nat
ctx: Vec Ty a✝a✝ + 1 < a✝Goals accomplished! 🐙fact.fact: {a : Nat} → {ctx : Vec Ty a} → Expr ctx (Ty.int.fn Ty.int)interpinterp: {a : Nat} → {ctx : Vec Ty a} → {ty : Ty} → Env ctx → Expr ctx ty → ty.interpEnv.nilEnv.nil: Env Vec.nil1010: Ty.int.interp
Dependent de Bruijn Indices
In this example, we represent program syntax terms in a type family parameterized by a list of types, representing the typing context, or information on which free variables are in scope and what their types are.
Remark: this example is based on an example in the book Certified Programming with Dependent Types by Adam Chlipala.
Programmers who move to statically typed functional languages from scripting languages often complain about the requirement that every element of a list have the same type. With fancy type systems, we can partially lift this requirement. We can index a list type with a “type-level” list that explains what type each element of the list should have. This has been done in a variety of ways in Haskell using type classes, and we can do it much more cleanly and directly in Lean.
We parameterize our heterogeneous lists by at type α and an α-indexed type β.
inductive HList: {α : Type v} → (α → Type u) → List α → Type (max u v)
HList {α: Type v
α : Type v: Type (v + 1)
Type v} (β: α → Type u
β : α: Type v
α → Type u: Type (u + 1)
Type u) : List: Type v → Type v
List α: Type v
α → Type (max u v): Type ((max u v) + 1)
Type (max u v)
| nil: {α : Type v} → {β : α → Type u} → HList β []
nil : HList: {α : Type v} → (α → Type u) → List α → Type (max u v)
HList β: α → Type u
β []: List α
[]
| cons: {α : Type v} → {β : α → Type u} → {i : α} → {is : List α} → β i → HList β is → HList β (i :: is)
cons : β: α → Type u
β i: α
i → HList: {α : Type v} → (α → Type u) → List α → Type (max u v)
HList β: α → Type u
β is: List α
is → HList: {α : Type v} → (α → Type u) → List α → Type (max u v)
HList β: α → Type u
β (i: α
i::is: List α
is)
We overload the List.cons notation :: so we can also use it to create
heterogeneous lists.
infix:67 " :: " => HList.cons: {α : Type v} → {β : α → Type u} → {i : α} → {is : List α} → β i → HList β is → HList β (i :: is)
HList.cons
We similarly overload the List notation [] for the empty heterogeneous list.
notation "[" "]" => HList.nil: {α : Type v} → {β : α → Type u} → HList β []
HList.nil
Variables are represented in a way isomorphic to the natural numbers, where
number 0 represents the first element in the context, number 1 the second element, and so
on. Actually, instead of numbers, we use the Member inductive family.
The value of type Member a as can be viewed as a certificate that a is
an element of the list as. The constructor Member.head says that a
is in the list if the list begins with it. The constructor Member.tail
says that if a is in the list bs, it is also in the list b::bs.
inductive Member: {α : Type} → α → List α → Type
Member : α: Type
α → List: Type → Type
List α: Type
α → Type: Type 1
Type
| head: {α : Type} → {a : α} → {as : List α} → Member a (a :: as)
head : Member: {α : Type} → α → List α → Type
Member a: ?m.3897
a (a: ?m.3897
a::as: List ?m.3897
as)
| tail: {α : Type} → {a : α} → {bs : List α} → {b : α} → Member a bs → Member a (b :: bs)
tail : Member: {α : Type} → α → List α → Type
Member a: ?m.4079
a bs: List ?m.4079
bs → Member: {α : Type} → α → List α → Type
Member a: ?m.4079
a (b: ?m.4079
b::bs: List ?m.4079
bs)
Given a heterogeneous list HList β is and value of type Member i is, HList.get
retrieves an element of type β i from the list.
The pattern .head and .tail h are sugar for Member.head and Member.tail h respectively.
Lean can infer the namespace using the expected type.
defHList.get :HList.get: {α : Type} → {β : α → Type u_1} → {is : List α} → {i : α} → HList β is → Member i is → β iHListHList: {α : Type} → (α → Type u_1) → List α → Type u_1ββ: ?m.4706 → Type u_1is →is: List ?m.4706MemberMember: {α : Type} → α → List α → Typeii: ?m.4706is →is: List ?m.4706ββ: ?m.4706 → Type u_1i |i: ?m.4706a::a: β ias,as: HList β is✝.head =>.head: {α : Type} → {a : α} → {as : List α} → Member a (a :: as)a |a: β i::as,as: HList β is✝.tail.tail: {α : Type} → {a : α} → {bs : List α} → {b : α} → Member a bs → Member a (b :: bs)h =>h: Member i is✝as.as: HList β is✝getget: {α : Type} → {β : α → Type u_1} → {is : List α} → {i : α} → HList β is → Member i is → β ihh: Member i is✝
Here is the definition of the simple type system for our programming language, a simply typed lambda calculus with natural numbers as the base type.
inductive Ty: Type
Ty where
| nat: Ty
nat
| fn: Ty → Ty → Ty
fn : Ty: Type
Ty → Ty: Type
Ty → Ty: Type
Ty
We can write a function to translate Ty values to a Lean type
— remember that types are first class, so can be calculated just like any other value.
We mark Ty.denote as [reducible] to make sure the typeclass resolution procedure can
unfold/reduce it. For example, suppose Lean is trying to synthesize a value for the instance
Add (Ty.denote Ty.nat). Since Ty.denote is marked as [reducible],
the typeclass resolution procedure can reduce Ty.denote Ty.nat to Nat, and use
the builtin instance for Add Nat as the solution.
Recall that the term a.denote is sugar for denote a where denote is the function being defined.
We call it the "dot notation".
@[reducible] def Ty.denote: Ty → Type
Ty.denote : Ty: Type
Ty → Type: Type 1
Type
| nat: Ty
nat => Nat: Type
Nat
| fn: Ty → Ty → Ty
fn a: Ty
a b: Ty
b => a: Ty
a.denote: Ty → Type
denote → b: Ty
b.denote: Ty → Type
denote
Here is the definition of the Term type, including variables, constants, addition,
function application and abstraction, and let binding of local variables.
Since let is a keyword in Lean, we use the "escaped identifier" «let».
You can input the unicode (French double quotes) using \f<< (for «) and \f>> (for »).
The term Term ctx .nat is sugar for Term ctx Ty.nat, Lean infers the namespace using the expected type.
inductive Term: List Ty → Ty → Type
Term : List: Type → Type
List Ty: Type
Ty → Ty: Type
Ty → Type: Type 1
Type
| var: {ty : Ty} → {ctx : List Ty} → Member ty ctx → Term ctx ty
var : Member: {α : Type} → α → List α → Type
Member ty: Ty
ty ctx: List Ty
ctx → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ty: Ty
ty
| const: {ctx : List Ty} → Nat → Term ctx Ty.nat
const : Nat: Type
Nat → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx .nat: Ty
.nat
| plus: {ctx : List Ty} → Term ctx Ty.nat → Term ctx Ty.nat → Term ctx Ty.nat
plus : Term: List Ty → Ty → Type
Term ctx: List Ty
ctx .nat: Ty
.nat → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx .nat: Ty
.nat → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx .nat: Ty
.nat
| app: {ctx : List Ty} → {dom ran : Ty} → Term ctx (dom.fn ran) → Term ctx dom → Term ctx ran
app : Term: List Ty → Ty → Type
Term ctx: List Ty
ctx (.fn: Ty → Ty → Ty
.fn dom: Ty
dom ran: Ty
ran) → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx dom: Ty
dom → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ran: Ty
ran
| lam: {dom : Ty} → {ctx : List Ty} → {ran : Ty} → Term (dom :: ctx) ran → Term ctx (dom.fn ran)
lam : Term: List Ty → Ty → Type
Term (dom: Ty
dom :: ctx: List Ty
ctx) ran: Ty
ran → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx (.fn: Ty → Ty → Ty
.fn dom: Ty
dom ran: Ty
ran)
| «let»: {ctx : List Ty} → {ty₁ ty₂ : Ty} → Term ctx ty₁ → Term (ty₁ :: ctx) ty₂ → Term ctx ty₂
«let» : Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ty₁: Ty
ty₁ → Term: List Ty → Ty → Type
Term (ty₁: Ty
ty₁ :: ctx: List Ty
ctx) ty₂: Ty
ty₂ → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ty₂: Ty
ty₂
Here are two example terms encoding, the first addition packaged as a two-argument curried function, and the second of a sample application of addition to constants.
The command open Ty Term Member opens the namespaces Ty, Term, and Member. Thus,
you can write lam instead of Term.lam.
open Ty Term Member
def add: Term [] (nat.fn (nat.fn nat))
add : Term: List Ty → Ty → Type
Term []: List Ty
[] (fn: Ty → Ty → Ty
fn nat: Ty
nat (fn: Ty → Ty → Ty
fn nat: Ty
nat nat: Ty
nat)) :=
lam: {dom : Ty} → {ctx : List Ty} → {ran : Ty} → Term (dom :: ctx) ran → Term ctx (dom.fn ran)
lam (lam: {dom : Ty} → {ctx : List Ty} → {ran : Ty} → Term (dom :: ctx) ran → Term ctx (dom.fn ran)
lam (plus: {ctx : List Ty} → Term ctx nat → Term ctx nat → Term ctx nat
plus (var: {ty : Ty} → {ctx : List Ty} → Member ty ctx → Term ctx ty
var (tail: {α : Type} → {a : α} → {bs : List α} → {b : α} → Member a bs → Member a (b :: bs)
tail head: {α : Type} → {a : α} → {as : List α} → Member a (a :: as)
head)) (var: {ty : Ty} → {ctx : List Ty} → Member ty ctx → Term ctx ty
var head: {α : Type} → {a : α} → {as : List α} → Member a (a :: as)
head)))
def three_the_hard_way: Term [] nat
three_the_hard_way : Term: List Ty → Ty → Type
Term []: List Ty
[] nat: Ty
nat :=
app: {ctx : List Ty} → {dom ran : Ty} → Term ctx (dom.fn ran) → Term ctx dom → Term ctx ran
app (app: {ctx : List Ty} → {dom ran : Ty} → Term ctx (dom.fn ran) → Term ctx dom → Term ctx ran
app add: Term [] (nat.fn (nat.fn nat))
add (const: {ctx : List Ty} → Nat → Term ctx nat
const 1: Nat
1)) (const: {ctx : List Ty} → Nat → Term ctx nat
const 2: Nat
2)
Since dependent typing ensures that any term is well-formed in its context and has a particular type, it is easy to translate syntactic terms into Lean values.
The attribute [simp] instructs Lean to always try to unfold Term.denote applications when one applies
the simp tactic. We also say this is a hint for the Lean term simplifier.
@[simp] def Term.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
Term.denote : Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ty: Ty
ty → HList: {α : Type} → (α → Type) → List α → Type
HList Ty.denote: Ty → Type
Ty.denote ctx: List Ty
ctx → ty: Ty
ty.denote: Ty → Type
denote
| var: {ty : Ty} → {ctx : List Ty} → Member ty ctx → Term ctx ty
var h: Member ty ctx
h, env: HList Ty.denote ctx
env => env: HList Ty.denote ctx
env.get: {α : Type} → {β : α → Type} → {is : List α} → {i : α} → HList β is → Member i is → β i
get h: Member ty ctx
h
| const: {ctx : List Ty} → Nat → Term ctx nat
const n: Nat
n, _ => n: Nat
n
| plus: {ctx : List Ty} → Term ctx nat → Term ctx nat → Term ctx nat
plus a: Term ctx nat
a b: Term ctx nat
b, env: HList Ty.denote ctx
env => a: Term ctx nat
a.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote env: HList Ty.denote ctx
env + b: Term ctx nat
b.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote env: HList Ty.denote ctx
env
| app: {ctx : List Ty} → {dom ran : Ty} → Term ctx (dom.fn ran) → Term ctx dom → Term ctx ran
app f: Term ctx (dom✝.fn ty)
f a: Term ctx dom✝
a, env: HList Ty.denote ctx
env => f: Term ctx (dom✝.fn ty)
f.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote env: HList Ty.denote ctx
env (a: Term ctx dom✝
a.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote env: HList Ty.denote ctx
env)
| lam: {dom : Ty} → {ctx : List Ty} → {ran : Ty} → Term (dom :: ctx) ran → Term ctx (dom.fn ran)
lam b: Term (dom✝ :: ctx) ran✝
b, env: HList Ty.denote ctx
env => fun x: dom✝.denote
x => b: Term (dom✝ :: ctx) ran✝
b.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote (x: dom✝.denote
x :: env: HList Ty.denote ctx
env)
| «let»: {ctx : List Ty} → {ty₁ ty₂ : Ty} → Term ctx ty₁ → Term (ty₁ :: ctx) ty₂ → Term ctx ty₂
«let» a: Term ctx ty₁✝
a b: Term (ty₁✝ :: ctx) ty
b, env: HList Ty.denote ctx
env => b: Term (ty₁✝ :: ctx) ty
b.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote (a: Term ctx ty₁✝
a.denote: {ctx : List Ty} → {ty : Ty} → Term ctx ty → HList Ty.denote ctx → ty.denote
denote env: HList Ty.denote ctx
env :: env: HList Ty.denote ctx
env)
You can show that the denotation of three_the_hard_way is indeed 3 using reflexivity.
We now define the constant folding optimization that traverses a term if replaces subterms such as
plus (const m) (const n) with const (n+m).
@[simp] def Term.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
Term.constFold : Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ty: Ty
ty → Term: List Ty → Ty → Type
Term ctx: List Ty
ctx ty: Ty
ty
| const: {ctx : List Ty} → Nat → Term ctx nat
const n: Nat
n => const: {ctx : List Ty} → Nat → Term ctx nat
const n: Nat
n
| var: {ty : Ty} → {ctx : List Ty} → Member ty ctx → Term ctx ty
var h: Member ty ctx
h => var: {ty : Ty} → {ctx : List Ty} → Member ty ctx → Term ctx ty
var h: Member ty ctx
h
| app: {ctx : List Ty} → {dom ran : Ty} → Term ctx (dom.fn ran) → Term ctx dom → Term ctx ran
app f: Term ctx (dom✝.fn ty)
f a: Term ctx dom✝
a => app: {ctx : List Ty} → {dom ran : Ty} → Term ctx (dom.fn ran) → Term ctx dom → Term ctx ran
app f: Term ctx (dom✝.fn ty)
f.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold a: Term ctx dom✝
a.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold
| lam: {dom : Ty} → {ctx : List Ty} → {ran : Ty} → Term (dom :: ctx) ran → Term ctx (dom.fn ran)
lam b: Term (dom✝ :: ctx) ran✝
b => lam: {dom : Ty} → {ctx : List Ty} → {ran : Ty} → Term (dom :: ctx) ran → Term ctx (dom.fn ran)
lam b: Term (dom✝ :: ctx) ran✝
b.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold
| «let»: {ctx : List Ty} → {ty₁ ty₂ : Ty} → Term ctx ty₁ → Term (ty₁ :: ctx) ty₂ → Term ctx ty₂
«let» a: Term ctx ty₁✝
a b: Term (ty₁✝ :: ctx) ty
b => «let»: {ctx : List Ty} → {ty₁ ty₂ : Ty} → Term ctx ty₁ → Term (ty₁ :: ctx) ty₂ → Term ctx ty₂
«let» a: Term ctx ty₁✝
a.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold b: Term (ty₁✝ :: ctx) ty
b.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold
| plus: {ctx : List Ty} → Term ctx nat → Term ctx nat → Term ctx nat
plus a: Term ctx nat
a b: Term ctx nat
b =>
match a: Term ctx nat
a.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold, b: Term ctx nat
b.constFold: {ctx : List Ty} → {ty : Ty} → Term ctx ty → Term ctx ty
constFold with
| const: {ctx : List Ty} → Nat → Term ctx nat
const n: Nat
n, const: {ctx : List Ty} → Nat → Term ctx nat
const m: Nat
m => const: {ctx : List Ty} → Nat → Term ctx nat
const (n: Nat
n+m: Nat
m)
| a': Term ctx nat
a', b': Term ctx nat
b' => plus: {ctx : List Ty} → Term ctx nat → Term ctx nat → Term ctx nat
plus a': Term ctx nat
a' b': Term ctx nat
b'
The correctness of the Term.constFold is proved using induction, case-analysis, and the term simplifier.
We prove all cases but the one for plus using simp [*]. This tactic instructs the term simplifier to
use hypotheses such as a = b as rewriting/simplifications rules.
We use the split to break the nested match expression in the plus case into two cases.
The local variables iha and ihb are the induction hypotheses for a and b.
The modifier ← in a term simplifier argument instructs the term simplifier to use the equation as a rewriting rule in
the "reverse direction". That is, given h : a = b, ← h instructs the term simplifier to rewrite b subterms to a.
Goals accomplished! 🐙ctx: List Ty
ty: Ty
env: HList Ty.denote ctx
e: Term ctx tye.constFold.denote env = e.denote envGoals accomplished! 🐙Goals accomplished! 🐙ctx: List Ty
ty: Ty
ctx✝: List Ty
a, b: Term ctx✝ nat
iha: ∀ {env : HList Ty.denote ctx✝}, a.constFold.denote env = a.denote env
ihb: ∀ {env : HList Ty.denote ctx✝}, b.constFold.denote env = b.denote env
env: HList Ty.denote ctx✝
x✝¹, x✝: Term ctx✝ nat
n✝, m✝: Nat
heq✝¹: a.constFold = const n✝
heq✝: b.constFold = const m✝
plus.h_1(const (n✝ + m✝)).denote env = a.denote env + b.denote envctx: List Ty
ty: Ty
ctx✝: List Ty
a, b: Term ctx✝ nat
iha: ∀ {env : HList Ty.denote ctx✝}, a.constFold.denote env = a.denote env
ihb: ∀ {env : HList Ty.denote ctx✝}, b.constFold.denote env = b.denote env
env: HList Ty.denote ctx✝
x✝², x✝¹: Term ctx✝ nat
x✝: ∀ (n m : Nat), a.constFold = const n → b.constFold = const m → False(a.constFold.plus b.constFold).denote env = a.denote env + b.denote envctx: List Ty
ty: Ty
ctx✝: List Ty
a, b: Term ctx✝ nat
iha: ∀ {env : HList Ty.denote ctx✝}, a.constFold.denote env = a.denote env
ihb: ∀ {env : HList Ty.denote ctx✝}, b.constFold.denote env = b.denote env
env: HList Ty.denote ctx✝
x✝¹, x✝: Term ctx✝ nat
n✝, m✝: Nat
heq✝¹: a.constFold = const n✝
heq✝: b.constFold = const m✝
plus.h_1(const (n✝ + m✝)).denote env = a.denote env + b.denote envctx: List Ty
ty: Ty
ctx✝: List Ty
a, b: Term ctx✝ nat
iha: ∀ {env : HList Ty.denote ctx✝}, a.constFold.denote env = a.denote env
ihb: ∀ {env : HList Ty.denote ctx✝}, b.constFold.denote env = b.denote env
env: HList Ty.denote ctx✝
x✝², x✝¹: Term ctx✝ nat
x✝: ∀ (n m : Nat), a.constFold = const n → b.constFold = const m → False(a.constFold.plus b.constFold).denote env = a.denote env + b.denote envGoals accomplished! 🐙ctx: List Ty
ty: Ty
ctx✝: List Ty
a, b: Term ctx✝ nat
iha: ∀ {env : HList Ty.denote ctx✝}, a.constFold.denote env = a.denote env
ihb: ∀ {env : HList Ty.denote ctx✝}, b.constFold.denote env = b.denote env
env: HList Ty.denote ctx✝
x✝², x✝¹: Term ctx✝ nat
x✝: ∀ (n m : Nat), a.constFold = const n → b.constFold = const m → False
plus.h_2(a.constFold.plus b.constFold).denote env = a.denote env + b.denote envGoals accomplished! 🐙
Parametric Higher-Order Abstract Syntax
In contrast to first-order encodings, higher-order encodings avoid explicit modeling of variable identity. Instead, the binding constructs of an object language (the language being formalized) can be represented using the binding constructs of the meta language (the language in which the formalization is done). The best known higher-order encoding is called higher-order abstract syntax (HOAS), and we can start by attempting to apply it directly in Lean.
Remark: this example is based on an example in the book Certified Programming with Dependent Types by Adam Chlipala.
Here is the definition of the simple type system for our programming language, a simply typed lambda calculus with natural numbers as the base type.
inductive Ty: Type
Ty where
| nat: Ty
nat
| fn: Ty → Ty → Ty
fn : Ty: Type
Ty → Ty: Type
Ty → Ty: Type
Ty
We can write a function to translate Ty values to a Lean type
— remember that types are first class, so can be calculated just like any other value.
We mark Ty.denote as [reducible] to make sure the typeclass resolution procedure can
unfold/reduce it. For example, suppose Lean is trying to synthesize a value for the instance
Add (Ty.denote Ty.nat). Since Ty.denote is marked as [reducible],
the typeclass resolution procedure can reduce Ty.denote Ty.nat to Nat, and use
the builtin instance for Add Nat as the solution.
Recall that the term a.denote is sugar for denote a where denote is the function being defined.
We call it the "dot notation".
@[reducible] def Ty.denote: Ty → Type
Ty.denote : Ty: Type
Ty → Type: Type 1
Type
| nat: Ty
nat => Nat: Type
Nat
| fn: Ty → Ty → Ty
fn a: Ty
a b: Ty
b => a: Ty
a.denote: Ty → Type
denote → b: Ty
b.denote: Ty → Type
denote
With HOAS, each object language binding construct is represented with a function of
the meta language. Here is what we get if we apply that idea within an inductive definition
of term syntax. However a naive encondig in Lean fails to meet the strict positivity restrictions
imposed by the Lean kernel. An alternate higher-order encoding is parametric HOAS, as introduced by Washburn
and Weirich for Haskell and tweaked by Adam Chlipala for use in Coq. The key idea is to parameterize the
declaration by a type family rep standing for a "representation of variables."
inductive Term': (Ty → Type) → Ty → Type
Term' (rep: Ty → Type
rep : Ty: Type
Ty → Type: Type 1
Type) : Ty: Type
Ty → Type: Type 1
Type
| var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
var : rep: Ty → Type
rep ty: Ty
ty → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty: Ty
ty
| const: {rep : Ty → Type} → Nat → Term' rep Ty.nat
const : Nat: Type
Nat → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep .nat: Ty
.nat
| plus: {rep : Ty → Type} → Term' rep Ty.nat → Term' rep Ty.nat → Term' rep Ty.nat
plus : Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep .nat: Ty
.nat → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep .nat: Ty
.nat → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep .nat: Ty
.nat
| lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
lam : (rep: Ty → Type
rep dom: Ty
dom → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ran: Ty
ran) → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep (.fn: Ty → Ty → Ty
.fn dom: Ty
dom ran: Ty
ran)
| app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
app : Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep (.fn: Ty → Ty → Ty
.fn dom: Ty
dom ran: Ty
ran) → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep dom: Ty
dom → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ran: Ty
ran
| let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂
let : Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty₁: Ty
ty₁ → (rep: Ty → Type
rep ty₁: Ty
ty₁ → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty₂: Ty
ty₂) → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty₂: Ty
ty₂
Lean accepts this definition because our embedded functions now merely take variables as
arguments, instead of arbitrary terms. One might wonder whether there is an easy loophole
to exploit here, instantiating the parameter rep as term itself. However, to do that, we
would need to choose a variable representation for this nested mention of term, and so on
through an infinite descent into term arguments.
We write the final type of a closed term using polymorphic quantification over all possible
choices of rep type family
open Ty (nat: Ty
nat fn: Ty → Ty → Ty
fn)
namespace FirstTry
def Term: Ty → Type 1
Term (ty: Ty
ty : Ty: Type
Ty) := (rep: Ty → Type
rep : Ty: Type
Ty → Type: Type 1
Type) → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty: Ty
ty
In the next two example, note how each is written as a function over a rep choice,
such that the specific choice has no impact on the structure of the term.
def add: Term (nat.fn (nat.fn nat))
add : Term: Ty → Type 1
Term (fn: Ty → Ty → Ty
fn nat: Ty
nat (fn: Ty → Ty → Ty
fn nat: Ty
nat nat: Ty
nat)) := fun _rep: Ty → Type
_rep =>
.lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam fun x: _rep nat
x => .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam fun y: _rep nat
y => .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus (.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var x: _rep nat
x) (.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var y: _rep nat
y)
def three_the_hard_way: Term nat
three_the_hard_way : Term: Ty → Type 1
Term nat: Ty
nat := fun rep: Ty → Type
rep =>
.app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app (.app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app (add: Term (nat.fn (nat.fn nat))
add rep: Ty → Type
rep) (.const: {rep : Ty → Type} → Nat → Term' rep nat
.const 1: Nat
1)) (.const: {rep : Ty → Type} → Nat → Term' rep nat
.const 2: Nat
2)
end FirstTry
The argument rep does not even appear in the function body for add. How can that be?
By giving our terms expressive types, we allow Lean to infer many arguments for us. In fact,
we do not even need to name the rep argument! By using Lean implicit arguments and lambdas,
we can completely hide rep in these examples.
def Term: Ty → Type 1
Term (ty: Ty
ty : Ty: Type
Ty) := {rep: Ty → Type
rep : Ty: Type
Ty → Type: Type 1
Type} → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty: Ty
ty
def add: Term (nat.fn (nat.fn nat))
add : Term: Ty → Type 1
Term (fn: Ty → Ty → Ty
fn nat: Ty
nat (fn: Ty → Ty → Ty
fn nat: Ty
nat nat: Ty
nat)) :=
.lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam fun x: rep✝ nat
x => .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam fun y: rep✝ nat
y => .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus (.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var x: rep✝ nat
x) (.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var y: rep✝ nat
y)
def three_the_hard_way: Term nat
three_the_hard_way : Term: Ty → Type 1
Term nat: Ty
nat :=
.app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app (.app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app add: Term (nat.fn (nat.fn nat))
add (.const: {rep : Ty → Type} → Nat → Term' rep nat
.const 1: Nat
1)) (.const: {rep : Ty → Type} → Nat → Term' rep nat
.const 2: Nat
2)
It may not be at all obvious that the PHOAS representation admits the crucial computable
operations. The key to effective deconstruction of PHOAS terms is one principle: treat
the rep parameter as an unconstrained choice of which data should be annotated on each
variable. We will begin with a simple example, that of counting how many variable nodes
appear in a PHOAS term. This operation requires no data annotated on variables, so we
simply annotate variables with Unit values. Note that, when we go under binders in the
cases for lam and let, we must provide the data value to annotate on the new variable we
pass beneath. For our current choice of Unit data, we always pass ().
def countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars : Term': (Ty → Type) → Ty → Type
Term' (fun _: Ty
_ => Unit: Type
Unit) ty: Ty
ty → Nat: Type
Nat
| .var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var _ => 1: Nat
1
| .const: {rep : Ty → Type} → Nat → Term' rep nat
.const _ => 0: Nat
0
| .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus a: Term' (fun x => Unit) nat
a b: Term' (fun x => Unit) nat
b => countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars a: Term' (fun x => Unit) nat
a + countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars b: Term' (fun x => Unit) nat
b
| .app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app f: Term' (fun x => Unit) (dom✝.fn ty)
f a: Term' (fun x => Unit) dom✝
a => countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars f: Term' (fun x => Unit) (dom✝.fn ty)
f + countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars a: Term' (fun x => Unit) dom✝
a
| .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam b: Unit → Term' (fun x => Unit) ran✝
b => countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars (b: Unit → Term' (fun x => Unit) ran✝
b (): Unit
())
| .let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂
.let a: Term' (fun x => Unit) ty₁✝
a b: Unit → Term' (fun x => Unit) ty
b => countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars a: Term' (fun x => Unit) ty₁✝
a + countVars: {ty : Ty} → Term' (fun x => Unit) ty → Nat
countVars (b: Unit → Term' (fun x => Unit) ty
b (): Unit
())
We can now easily prove that add has two variables by using reflexivity
Here is another example, translating PHOAS terms into strings giving a first-order rendering.
To implement this translation, the key insight is to tag variables with strings, giving their names.
The function takes as an additional input i which is used to create variable names for binders.
We also use the string interpolation available in Lean. For example, s!"x_{i}" is expanded to
"x_" ++ toString i.
defpretty (pretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringe :e: Term' (fun x => String) tyTerm' (funTerm': (Ty → Type) → Ty → Type_ =>_: TyString)String: Typety) (ty: Tyi :i: optParam Nat 1Nat :=Nat: Type1) :1: NatString := matchString: Typee with |e: Term' (fun x => String) ty.var.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep tys =>s: Strings |s: String.const.const: {rep : Ty → Type} → Nat → Term' rep natn =>n: NattoStringtoString: {α : Type} → [self : ToString α] → α → Stringn |n: Nat.app.app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ranff: Term' (fun x => String) (dom✝.fn ty)a => s!"({a: Term' (fun x => String) dom✝prettypretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringff: Term' (fun x => String) (dom✝.fn ty)i} {i: optParam Nat 1prettypretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringaa: Term' (fun x => String) dom✝i})" |i: optParam Nat 1.plus.plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nataa: Term' (fun x => String) natb => s!"({b: Term' (fun x => String) natprettypretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringaa: Term' (fun x => String) nati} + {i: optParam Nat 1prettypretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringbb: Term' (fun x => String) nati})" |i: optParam Nat 1.lam.lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)f => letf: String → Term' (fun x => String) ran✝x := s!"x_{x: Stringi}" s!"(fun {i: optParam Nat 1x} => {x: Stringpretty (pretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringff: String → Term' (fun x => String) ran✝x) (x: Stringi+i: optParam Nat 11)})" |1: Nat.let.let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂aa: Term' (fun x => String) ty₁✝b => letb: String → Term' (fun x => String) tyx := s!"x_{x: Stringi}" s!"(let {i: optParam Nat 1x} := {x: Stringprettypretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringaa: Term' (fun x => String) ty₁✝i}; => {i: optParam Nat 1pretty (pretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringbb: String → Term' (fun x => String) tyx) (x: Stringi+i: optParam Nat 11)}"1: Natprettypretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringthree_the_hard_waythree_the_hard_way: Term nat
It is not necessary to convert to a different representation to support many common
operations on terms. For instance, we can implement substitution of terms for variables.
The key insight here is to tag variables with terms, so that, on encountering a variable, we
can simply replace it by the term in its tag. We will call this function initially on a term
with exactly one free variable, tagged with the appropriate substitute. During recursion,
new variables are added, but they are only tagged with their own term equivalents. Note
that this function squash is parameterized over a specific rep choice.
def squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash : Term': (Ty → Type) → Ty → Type
Term' (Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep) ty: Ty
ty → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty: Ty
ty
| .var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var e: Term' rep ty
e => e: Term' rep ty
e
| .const: {rep : Ty → Type} → Nat → Term' rep nat
.const n: Nat
n => .const: {rep : Ty → Type} → Nat → Term' rep nat
.const n: Nat
n
| .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus a: Term' (Term' rep) nat
a b: Term' (Term' rep) nat
b => .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus (squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash a: Term' (Term' rep) nat
a) (squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash b: Term' (Term' rep) nat
b)
| .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam f: Term' rep dom✝ → Term' (Term' rep) ran✝
f => .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam fun x: rep dom✝
x => squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash (f: Term' rep dom✝ → Term' (Term' rep) ran✝
f (.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var x: rep dom✝
x))
| .app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app f: Term' (Term' rep) (dom✝.fn ty)
f a: Term' (Term' rep) dom✝
a => .app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app (squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash f: Term' (Term' rep) (dom✝.fn ty)
f) (squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash a: Term' (Term' rep) dom✝
a)
| .let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂
.let a: Term' (Term' rep) ty₁✝
a b: Term' rep ty₁✝ → Term' (Term' rep) ty
b => .let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂
.let (squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash a: Term' (Term' rep) ty₁✝
a) fun x: rep ty₁✝
x => squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash (b: Term' rep ty₁✝ → Term' (Term' rep) ty
b (.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var x: rep ty₁✝
x))
To define the final substitution function over terms with single free variables, we define
Term1, an analogue to Term that we defined before for closed terms.
def Term1: Ty → Ty → Type 1
Term1 (ty1: Ty
ty1 ty2: Ty
ty2 : Ty: Type
Ty) := {rep: Ty → Type
rep : Ty: Type
Ty → Type: Type 1
Type} → rep: Ty → Type
rep ty1: Ty
ty1 → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty2: Ty
ty2
Substitution is defined by (1) instantiating a Term1 to tag variables with terms and (2)
applying the result to a specific term to be substituted. Note how the parameter rep of
squash is instantiated: the body of subst is itself a polymorphic quantification over rep,
standing for a variable tag choice in the output term; and we use that input to compute a
tag choice for the input term.
def subst: {ty1 ty2 : Ty} → Term1 ty1 ty2 → Term ty1 → Term ty2
subst (e: Term1 ty1 ty2
e : Term1: Ty → Ty → Type 1
Term1 ty1: Ty
ty1 ty2: Ty
ty2) (e': Term ty1
e' : Term: Ty → Type 1
Term ty1: Ty
ty1) : Term: Ty → Type 1
Term ty2: Ty
ty2 :=
squash: {rep : Ty → Type} → {ty : Ty} → Term' (Term' rep) ty → Term' rep ty
squash (e: Term1 ty1 ty2
e e': Term ty1
e')
We can view Term1 as a term with hole. In the following example,
(fun x => plus (var x) (const 5)) can be viewed as the term plus _ (const 5) where
the hole _ is instantiated by subst with three_the_hard_way
pretty <|pretty: {ty : Ty} → Term' (fun x => String) ty → optParam Nat 1 → Stringsubst (funsubst: {ty1 ty2 : Ty} → Term1 ty1 ty2 → Term ty1 → Term ty2x =>x: rep✝ nat.plus (.plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat.var.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep tyx) (x: rep✝ nat.const.const: {rep : Ty → Type} → Nat → Term' rep nat5))5: Natthree_the_hard_waythree_the_hard_way: Term nat
One further development, which may seem surprising at first, is that we can also implement a usual term denotation function, when we tag variables with their denotations.
The attribute [simp] instructs Lean to always try to unfold denote applications when one applies
the simp tactic. We also say this is a hint for the Lean term simplifier.
@[simp] defdenote :denote: {ty : Ty} → Term' Ty.denote ty → ty.denoteTerm'Term': (Ty → Type) → Ty → TypeTy.denoteTy.denote: Ty → Typety →ty: Tyty.ty: Tydenote |denote: Ty → Type.var.var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep tyx =>x: ty.denotex |x: ty.denote.const.const: {rep : Ty → Type} → Nat → Term' rep natn =>n: Natn |n: Nat.plus.plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nataa: Term' Ty.denote natb =>b: Term' Ty.denote natdenotedenote: {ty : Ty} → Term' Ty.denote ty → ty.denotea +a: Term' Ty.denote natdenotedenote: {ty : Ty} → Term' Ty.denote ty → ty.denoteb |b: Term' Ty.denote nat.app.app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ranff: Term' Ty.denote (dom✝.fn ty)a =>a: Term' Ty.denote dom✝denotedenote: {ty : Ty} → Term' Ty.denote ty → ty.denotef (f: Term' Ty.denote (dom✝.fn ty)denotedenote: {ty : Ty} → Term' Ty.denote ty → ty.denotea) |a: Term' Ty.denote dom✝.lam.lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)f => funf: dom✝.denote → Term' Ty.denote ran✝x =>x: dom✝.denotedenote (denote: {ty : Ty} → Term' Ty.denote ty → ty.denoteff: dom✝.denote → Term' Ty.denote ran✝x) |x: dom✝.denote.let.let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂aa: Term' Ty.denote ty₁✝b =>b: ty₁✝.denote → Term' Ty.denote tydenote (denote: {ty : Ty} → Term' Ty.denote ty → ty.denoteb (b: ty₁✝.denote → Term' Ty.denote tydenotedenote: {ty : Ty} → Term' Ty.denote ty → ty.denotea))a: Term' Ty.denote ty₁✝
To summarize, the PHOAS representation has all the expressive power of more standard encodings (e.g., using de Bruijn indices), and a variety of translations are actually much more pleasant to implement than usual, thanks to the novel ability to tag variables with data.
We now define the constant folding optimization that traverses a term if replaces subterms such as
plus (const m) (const n) with const (n+m).
@[simp] def constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold : Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty: Ty
ty → Term': (Ty → Type) → Ty → Type
Term' rep: Ty → Type
rep ty: Ty
ty
| .var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var x: rep ty
x => .var: {rep : Ty → Type} → {ty : Ty} → rep ty → Term' rep ty
.var x: rep ty
x
| .const: {rep : Ty → Type} → Nat → Term' rep nat
.const n: Nat
n => .const: {rep : Ty → Type} → Nat → Term' rep nat
.const n: Nat
n
| .app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app f: Term' rep (dom✝.fn ty)
f a: Term' rep dom✝
a => .app: {rep : Ty → Type} → {dom ran : Ty} → Term' rep (dom.fn ran) → Term' rep dom → Term' rep ran
.app (constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold f: Term' rep (dom✝.fn ty)
f) (constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold a: Term' rep dom✝
a)
| .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam f: rep dom✝ → Term' rep ran✝
f => .lam: {rep : Ty → Type} → {dom ran : Ty} → (rep dom → Term' rep ran) → Term' rep (dom.fn ran)
.lam fun x: rep dom✝
x => constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold (f: rep dom✝ → Term' rep ran✝
f x: rep dom✝
x)
| .let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂
.let a: Term' rep ty₁✝
a b: rep ty₁✝ → Term' rep ty
b => .let: {rep : Ty → Type} → {ty₁ ty₂ : Ty} → Term' rep ty₁ → (rep ty₁ → Term' rep ty₂) → Term' rep ty₂
.let (constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold a: Term' rep ty₁✝
a) fun x: rep ty₁✝
x => constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold (b: rep ty₁✝ → Term' rep ty
b x: rep ty₁✝
x)
| .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus a: Term' rep nat
a b: Term' rep nat
b =>
match constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold a: Term' rep nat
a, constFold: {rep : Ty → Type} → {ty : Ty} → Term' rep ty → Term' rep ty
constFold b: Term' rep nat
b with
| .const: {rep : Ty → Type} → Nat → Term' rep nat
.const n: Nat
n, .const: {rep : Ty → Type} → Nat → Term' rep nat
.const m: Nat
m => .const: {rep : Ty → Type} → Nat → Term' rep nat
.const (n: Nat
n+m: Nat
m)
| a': Term' rep nat
a', b': Term' rep nat
b' => .plus: {rep : Ty → Type} → Term' rep nat → Term' rep nat → Term' rep nat
.plus a': Term' rep nat
a' b': Term' rep nat
b'
The correctness of the constFold is proved using induction, case-analysis, and the term simplifier.
We prove all cases but the one for plus using simp [*]. This tactic instructs the term simplifier to
use hypotheses such as a = b as rewriting/simplifications rules.
We use the split to break the nested match expression in the plus case into two cases.
The local variables iha and ihb are the induction hypotheses for a and b.
The modifier ← in a term simplifier argument instructs the term simplifier to use the equation as a rewriting rule in
the "reverse direction. That is, given h : a = b, ← h instructs the term simplifier to rewrite b subterms to a.
Goals accomplished! 🐙ty: Ty
e: Term' Ty.denote tydenote (constFold e) = denote ety: Ty
a, b: Term' Ty.denote nat
iha: denote (constFold a) = denote a
ihb: denote (constFold b) = denote b
plusdenote (match constFold a, constFold b with | Term'.const n, Term'.const m => Term'.const (n + m) | a', b' => a'.plus b') = denote a + denote bGoals accomplished! 🐙ty: Ty
a, b: Term' Ty.denote nat
iha: denote (constFold a) = denote a
ihb: denote (constFold b) = denote b
x✝¹, x✝: Term' Ty.denote nat
n✝, m✝: Nat
heq✝¹: constFold a = Term'.const n✝
heq✝: constFold b = Term'.const m✝
plus.h_1denote (Term'.const (n✝ + m✝)) = denote a + denote bty: Ty
a, b: Term' Ty.denote nat
iha: denote (constFold a) = denote a
ihb: denote (constFold b) = denote b
x✝², x✝¹: Term' Ty.denote nat
x✝: ∀ (n m : Nat), constFold a = Term'.const n → constFold b = Term'.const m → Falsedenote ((constFold a).plus (constFold b)) = denote a + denote bty: Ty
a, b: Term' Ty.denote nat
iha: denote (constFold a) = denote a
ihb: denote (constFold b) = denote b
x✝¹, x✝: Term' Ty.denote nat
n✝, m✝: Nat
heq✝¹: constFold a = Term'.const n✝
heq✝: constFold b = Term'.const m✝
plus.h_1denote (Term'.const (n✝ + m✝)) = denote a + denote bty: Ty
a, b: Term' Ty.denote nat
iha: denote (constFold a) = denote a
ihb: denote (constFold b) = denote b
x✝², x✝¹: Term' Ty.denote nat
x✝: ∀ (n m : Nat), constFold a = Term'.const n → constFold b = Term'.const m → Falsedenote ((constFold a).plus (constFold b)) = denote a + denote bGoals accomplished! 🐙ty: Ty
a, b: Term' Ty.denote nat
iha: denote (constFold a) = denote a
ihb: denote (constFold b) = denote b
x✝², x✝¹: Term' Ty.denote nat
x✝: ∀ (n m : Nat), constFold a = Term'.const n → constFold b = Term'.const m → False
plus.h_2denote ((constFold a).plus (constFold b)) = denote a + denote bGoals accomplished! 🐙
Syntax Metaprogramming Examples
Balanced Parentheses as an Embedded Domain Specific Language
Let's look at how to use macros to extend the Lean 4 parser and embed a language for building balanced parentheses. This language accepts strings given by the BNF grammar
Dyck ::=
"(" Dyck ")"
| "{" Dyck "}"
| end
We begin by defining an inductive data type of the grammar we wish to parse:
inductive Dyck : Type where
| round : Dyck → Dyck -- ( <inner> )
| curly : Dyck → Dyck -- { <inner> }
| leaf : Dyck
We begin by declaring a syntax category using the declare_syntax_cat <category> command.
This names our grammar and allows us to specify parsing rules associated with our grammar.
declare_syntax_cat brack
Next, we specify the grammar using the syntax <parse rule> command:
syntax "end" : brack
The above means that the token "end" lives in syntax category brack.
Similarly, we declare the rules "(" Dyck ")" and "{" Dyck "}" using the rules:
syntax "(" brack ")" : brack
syntax "{" brack "}" : brack
Finally, we need a way to build Lean 4 terms from this grammar -- that is, we must translate out of this
grammar into a Dyck value, which is a Lean 4 term. For this, we create a new kind of "quotation" that
consumes syntax in brack and produces a term.
syntax "`[Dyck| " brack "]" : term
To specify the transformation rules, we use macro_rules to declare how the syntax `[Dyck| <brack>]
produces terms. This is written using a pattern-matching style syntax, where the left-hand side
declares the syntax pattern to be matched, and the right-hand side declares the production. Syntax placeholders (antiquotations)
are introduced via the $<var-name> syntax. The right-hand side is
an arbitrary Lean term that we are producing.
macro_rules
| `(`[Dyck| end]) => `(Dyck.leaf)
| `(`[Dyck| ($b)]) => `(Dyck.round `[Dyck| $b]) -- recurse
| `(`[Dyck| {$b}]) => `(Dyck.curly `[Dyck| $b]) -- recurse
#check `[Dyck| end] -- Dyck.leaf
#check `[Dyck| {(end)}] -- Dyck.curl (Dyck.round Dyck.leaf)
In summary, we've seen:
- How to declare a syntax category for the Dyck grammar.
- How to specify parse trees of this grammar using
syntax - How to translate out of this grammar into Lean 4 terms using
macro_rules.
The full program listing is given below:
inductive Dyck : Type where
| round : Dyck → Dyck -- ( <inner> )
| curly : Dyck → Dyck -- { <inner> }
| leaf : Dyck
-- declare Dyck grammar parse trees
declare_syntax_cat brack
syntax "(" brack ")" : brack
syntax "{" brack "}" : brack
syntax "end" : brack
-- notation for translating `brack` into `term`
syntax "`[Dyck| " brack "]" : term
-- rules to translate Dyck grammar into inductive value of type Dyck
macro_rules
| `(`[Dyck| end]) => `(Dyck.leaf)
| `(`[Dyck| ($b)]) => `(Dyck.round `[Dyck| $b]) -- recurse
| `(`[Dyck| {$b}]) => `(Dyck.curly `[Dyck| $b]) -- recurse
-- tests
#check `[Dyck| end] -- Dyck.leaf
#check `[Dyck| {(end)}] -- Dyck.curl (Dyck.round Dyck.leaf)
Arithmetic as an embedded domain-specific language
Let's parse another classic grammar, the grammar of arithmetic expressions with addition, multiplication, integers, and variables. In the process, we'll learn how to:
- Convert identifiers such as
xinto strings within a macro. - add the ability to "escape" the macro context from within the macro. This is useful to interpret identifiers with their original meaning (predefined values) instead of their new meaning within a macro (treat as a symbol).
Let's begin with the simplest thing possible. We'll define an AST, and use operators + and * to denote
building an arithmetic AST.
Here's the AST that we will be parsing:
inductive Arith : Type
| add : Arith → Arith → Arith -- e + f
| mul : Arith → Arith → Arith -- e * f
| int : Int → Arith -- constant
| symbol : String → Arith -- variable
We declare a syntax category to describe the grammar that we will be parsing.
See that we control the precedence of + and * by writing syntax:50 for addition and syntax:60 for multiplication,
indicating that multiplication binds tighter than addition (higher the number, tighter the binding).
This allows us to declare precedence when defining new syntax.
declare_syntax_cat arith
syntax num : arith -- int for Arith.int
syntax str : arith -- strings for Arith.symbol
syntax:60 arith:60 "+" arith:61 : arith -- Arith.add
syntax:70 arith:70 "*" arith:71 : arith -- Arith.mul
syntax "(" arith ")" : arith -- parenthesized expressions
Further, if we look at syntax:60 arith:60 "+" arith:61 : arith, the
precedence declarations at arith:60 "+" arith:61 conveys that the left
argument must have precedence at least 60 or greater, and the right argument
must have precedence at least61 or greater. Note that this forces left
associativity. To understand this, let's compare two hypothetical parses:
-- syntax:60 arith:60 "+" arith:61 : arith -- Arith.add
-- a + b + c
(a:60 + b:61):60 + c
a + (b:60 + c:61):60
In the parse tree of a + (b:60 + c:61):60, we see that the right argument (b + c) is given the precedence 60. However,
the rule for addition expects the right argument to have a precedence of at least 61, as witnessed by the arith:61 at
the right-hand-side of syntax:60 arith:60 "+" arith:61 : arith. Thus, the rule syntax:60 arith:60 "+" arith:61 : arith
ensures that addition is left associative.
Since addition is declared arguments of precedence 60/61 and multiplication with 70/71, this causes multiplication to bind
tighter than addition. Once again, let's compare two hypothetical parses:
-- syntax:60 arith:60 "+" arith:61 : arith -- Arith.add
-- syntax:70 arith:70 "*" arith:71 : arith -- Arith.mul
-- a * b + c
a * (b:60 + c:61):60
(a:70 * b:71):70 + c
While parsing a * (b + c), (b + c) is assigned a precedence 60 by the addition rule. However, multiplication expects
the right argument to have precedence at least 71. Thus, this parse is invalid. In contrast, (a * b) + c assigns
a precedence of 70 to (a * b). This is compatible with addition which expects the left argument to have precedence
**at least 60 ** (70 is greater than 60). Thus, the string a * b + c is parsed as (a * b) + c.
For more details, please look at the Lean manual on syntax extensions.
To go from strings into Arith, we define a macro to
translate the syntax category arith into an Arith inductive value that
lives in term:
-- auxiliary notation for translating `arith` into `term`
syntax "`[Arith| " arith "]" : term
Our macro rules perform the "obvious" translation:
macro_rules
| `(`[Arith| $s:str]) => `(Arith.symbol $s)
| `(`[Arith| $num:num]) => `(Arith.int $num)
| `(`[Arith| $x + $y]) => `(Arith.add `[Arith| $x] `[Arith| $y])
| `(`[Arith| $x * $y]) => `(Arith.mul `[Arith| $x] `[Arith| $y])
| `(`[Arith| ($x)]) => `(`[Arith| $x])
And some examples:
#check `[Arith| "x" * "y"] -- mul
-- Arith.mul (Arith.symbol "x") (Arith.symbol "y")
#check `[Arith| "x" + "y"] -- add
-- Arith.add (Arith.symbol "x") (Arith.symbol "y")
#check `[Arith| "x" + 20] -- symbol + int
-- Arith.add (Arith.symbol "x") (Arith.int 20)
#check `[Arith| "x" + "y" * "z"] -- precedence
-- Arith.add (Arith.symbol "x") (Arith.mul (Arith.symbol "y") (Arith.symbol "z"))
#check `[Arith| "x" * "y" + "z"] -- precedence
-- Arith.add (Arith.mul (Arith.symbol "x") (Arith.symbol "y")) (Arith.symbol "z")
#check `[Arith| ("x" + "y") * "z"] -- parentheses
-- Arith.mul (Arith.add (Arith.symbol "x") (Arith.symbol "y")) (Arith.symbol "z")
Writing variables as strings, such as "x" gets old; wouldn't it be so much
prettier if we could write x * y, and have the macro translate this into Arith.mul (Arith.Symbol "x") (Arith.mul "y")?
We can do this, and this will be our first taste of manipulating macro variables --- we'll use x.getId instead of directly evaluating $x.
We also write a macro rule for Arith| that translates an identifier into
a string, using $(Lean.quote (toString x.getId)):
syntax ident : arith
macro_rules
| `(`[Arith| $x:ident]) => `(Arith.symbol $(Lean.quote (toString x.getId)))
Let's test and see that we can now write expressions such as x * y directly instead of having to write "x" * "y":
#check `[Arith| x] -- Arith.symbol "x"
def xPlusY := `[Arith| x + y]
#print xPlusY -- def xPlusY : Arith := Arith.add (Arith.symbol "x") (Arith.symbol "y")
We now show an unfortunate consequence of the above definitions. Suppose we want to build (x + y) + z.
Since we already have defined xPlusY as x + y, perhaps we should reuse it! Let's try:
#check `[Arith| xPlusY + z] -- Arith.add (Arith.symbol "xPlusY") (Arith.symbol "z")
Whoops, that didn't work! What happened? Lean treats xPlusY itself as an identifier! So we need to add some syntax
to be able to "escape" the Arith| context. Let's use the syntax <[ $e:term ]> to mean: evaluate $e as a real term,
not an identifier. The macro looks like follows:
syntax "<[" term "]>" : arith -- escape for embedding terms into `Arith`
macro_rules
| `(`[Arith| <[ $e:term ]>]) => pure e
Let's try our previous example:
#check `[Arith| <[ xPlusY ]> + z] -- Arith.add xPlusY (Arith.symbol "z")
Perfect!
In this tutorial, we expanded on the previous tutorial to parse a more realistic grammar with multiple levels of precedence, how to parse identifiers directly within a macro, and how to provide an escape from within the macro context.
Full code listing
inductive Arith : Type
| add : Arith → Arith → Arith -- e + f
| mul : Arith → Arith → Arith -- e * f
| int : Int → Arith -- constant
| symbol : String → Arith -- variable
declare_syntax_cat arith
syntax num : arith -- int for Arith.int
syntax str : arith -- strings for Arith.symbol
syntax:60 arith:60 "+" arith:61 : arith -- Arith.add
syntax:70 arith:70 "*" arith:71 : arith -- Arith.mul
syntax "(" arith ")" : arith -- parenthesized expressions
-- auxiliary notation for translating `arith` into `term`
syntax "`[Arith| " arith "]" : term
macro_rules
| `(`[Arith| $s:str]) => `(Arith.symbol $s)
| `(`[Arith| $num:num]) => `(Arith.int $num)
| `(`[Arith| $x + $y]) => `(Arith.add `[Arith| $x] `[Arith| $y])
| `(`[Arith| $x * $y]) => `(Arith.mul `[Arith| $x] `[Arith| $y])
| `(`[Arith| ($x)]) => `(`[Arith| $x])
#check `[Arith| "x" * "y"] -- mul
-- Arith.mul (Arith.symbol "x") (Arith.symbol "y")
#check `[Arith| "x" + "y"] -- add
-- Arith.add (Arith.symbol "x") (Arith.symbol "y")
#check `[Arith| "x" + 20] -- symbol + int
-- Arith.add (Arith.symbol "x") (Arith.int 20)
#check `[Arith| "x" + "y" * "z"] -- precedence
-- Arith.add (Arith.symbol "x") (Arith.mul (Arith.symbol "y") (Arith.symbol "z"))
#check `[Arith| "x" * "y" + "z"] -- precedence
-- Arith.add (Arith.mul (Arith.symbol "x") (Arith.symbol "y")) (Arith.symbol "z")
#check `[Arith| ("x" + "y") * "z"] -- parentheses
-- Arith.mul (Arith.add (Arith.symbol "x") (Arith.symbol "y")) (Arith.symbol "z")
syntax ident : arith
macro_rules
| `(`[Arith| $x:ident]) => `(Arith.symbol $(Lean.quote (toString x.getId)))
#check `[Arith| x] -- Arith.symbol "x"
def xPlusY := `[Arith| x + y]
#print xPlusY -- def xPlusY : Arith := Arith.add (Arith.symbol "x") (Arith.symbol "y")
syntax "<[" term "]>" : arith -- escape for embedding terms into `Arith`
macro_rules
| `(`[Arith| <[ $e:term ]>]) => pure e
#check `[Arith| <[ xPlusY ]> + z] -- Arith.add xPlusY (Arith.symbol "z")
The Lean Reference Manual
The latest version of the Lean reference manual is available here.
Frequently Asked Questions
What is Lean?
Lean is a new open source theorem prover being developed at Microsoft Research. It is a research project that aims to bridge the gap between interactive and automated theorem proving. Lean can be also used as a programming language. Actually, some Lean features are implemented in Lean itself.
Should I use Lean?
Lean is under heavy development, and we are constantly trying new ideas and tweaking the system. It is a research project and not a product. Things change rapidly, and we constantly break backward compatibility. Lean comes "as is", you should not expect we will fix bugs and/or add new features for your project. We have our own priorities, and will not change them to accommodate your needs. Even if you implement a new feature or fix a bug, we may not want to merge it because it may conflict with our plans for Lean, it may not be performant, we may not want to maintain it, we may be busy, etc. If you really need this new feature or bug fix, we suggest you create your own fork and maintain it yourself.
Where is the documentation?
This is the Lean 4 manual. It is a work in progress, but it will eventually cover the whole language. A public and very active chat room dedicated to Lean is open on Zulip. It is a good place to interact with other Lean users.
Should I use Lean to teach a course?
Lean has been used to teach courses on logic, type theory and programming languages at CMU and the University of Washington. The lecture notes for the CMU course Logic and Proof are available online, but they are for Lean 3. If you decide to teach a course using Lean, we suggest you prepare all material before the beginning of the course, and make sure that Lean attends all your needs. You should not expect we will fix bugs and/or add features needed for your course.
Are there IDEs for Lean?
Yes, see Setting Up Lean.
Is Lean sound? How big is the kernel? Should I trust it?
Lean has a relatively small kernel. Several independent checkers have been implemented for Lean 3. Two of them are tc and trepplein. We expect similar independent checkers will be built for Lean 4.
Should I open a new issue?
We use GitHub to track bugs and new features. Bug reports are always welcome, but nitpicking issues are not (e.g., the error message is confusing). See also our contribution guidelines.
Is it Lean, LEAN, or L∃∀N?
We always use "Lean" in writing. When specifying a major version number, we append it together with a single space: Lean 4.
Significant changes from Lean 3
Lean 4 is not backward compatible with Lean 3. We have rewritten most of the system, and took the opportunity to cleanup the syntax, metaprogramming framework, and elaborator. In this section, we go over the most significant changes.
Lambda expressions
We do not use , anymore to separate the binders from the lambda expression body.
The Lean 3 syntax for lambda expressions was unconventional, and , has been overused in Lean 3.
For example, we believe a list of lambda expressions is quite confusing in Lean 3, since , is used
to separate the elements of a list, and in the lambda expression itself. We now use => as the separator,
as an example, fun x => x is the identity function. One may still use the symbol λ as a shorthand for fun.
The lambda expression notation has many new features that are not supported in Lean 3.
Pattern matching
In Lean 4, one can easily create new notation that abbreviates commonly used idioms. One of them is a
fun followed by a match. In the following examples, we define a few functions using fun+match notation.
namespace ex1
def Prod.str : Nat × Nat → String :=
fun (a, b) => "(" ++ toString a ++ ", " ++ toString b ++ ")"
structure Point where
x : Nat
y : Nat
z : Nat
def Point.addX : Point → Point → Nat :=
fun { x := a, .. } { x := b, .. } => a+b
def Sum.str : Option Nat → String :=
fun
| some a => "some " ++ toString a
| none => "none"
end ex1
Implicit lambdas
In Lean 3 stdlib, we find many instances of the dreadful @+_ idiom.
It is often used when the expected type is a function type with implicit arguments,
and we have a constant (reader_t.pure in the example) which also takes implicit arguments. In Lean 4, the elaborator automatically introduces lambdas
for consuming implicit arguments. We are still exploring this feature and analyzing its impact, but the experience so far has been very positive. As an example,
here is the example in the link above using Lean 4 implicit lambdas.
variable (ρ : Type) (m : Type → Type) [Monad m]
instance : Monad (ReaderT ρ m) where
pure := ReaderT.pure
bind := ReaderT.bind
Users can disable the implicit lambda feature by using @ or writing a lambda expression with {} or [] binder annotations.
Here are few examples
namespace ex2
def id1 : {α : Type} → α → α :=
fun x => x
def listId : List ({α : Type} → α → α) :=
(fun x => x) :: []
-- In this example, implicit lambda introduction has been disabled because
-- we use `@` before `fun`
def id2 : {α : Type} → α → α :=
@fun α (x : α) => id1 x
def id3 : {α : Type} → α → α :=
@fun α x => id1 x
def id4 : {α : Type} → α → α :=
fun x => id1 x
-- In this example, implicit lambda introduction has been disabled
-- because we used the binder annotation `{...}`
def id5 : {α : Type} → α → α :=
fun {α} x => id1 x
end ex2
Sugar for simple functions
In Lean 3, we can create simple functions from infix operators by using parentheses. For example, (+1) is sugar for fun x, x + 1. In Lean 4, we generalize this notation using · as a placeholder. Here are a few examples:
namespace ex3
#check (· + 1)
-- fun a => a + 1
#check (2 - ·)
-- fun a => 2 - a
#eval [1, 2, 3, 4, 5].foldl (·*·) 1
-- 120
def f (x y z : Nat) :=
x + y + z
#check (f · 1 ·)
-- fun a b => f a 1 b
#eval [(1, 2), (3, 4), (5, 6)].map (·.1)
-- [1, 3, 5]
end ex3
As in Lean 3, the notation is activated using parentheses, and the lambda abstraction is created by collecting the nested ·s.
The collection is interrupted by nested parentheses. In the following example, two different lambda expressions are created.
#check (Prod.mk · (· + 1))
-- fun a => (a, fun b => b + 1)
Function applications
In Lean 4, we have support for named arguments. Named arguments enable you to specify an argument for a parameter by matching the argument with its name rather than with its position in the parameter list. If you don't remember the order of the parameters but know their names, you can send the arguments in any order. You may also provide the value for an implicit parameter when Lean failed to infer it. Named arguments also improve the readability of your code by identifying what each argument represents.
def sum (xs : List Nat) :=
xs.foldl (init := 0) (·+·)
#eval sum [1, 2, 3, 4]
-- 10
example {a b : Nat} {p : Nat → Nat → Nat → Prop} (h₁ : p a b b) (h₂ : b = a)
: p a a b :=
Eq.subst (motive := fun x => p a x b) h₂ h₁
In the following examples, we illustrate the interaction between named and default arguments.
def f (x : Nat) (y : Nat := 1) (w : Nat := 2) (z : Nat) :=
x + y + w - z
example (x z : Nat) : f (z := z) x = x + 1 + 2 - z := rfl
example (x z : Nat) : f x (z := z) = x + 1 + 2 - z := rfl
example (x y : Nat) : f x y = fun z => x + y + 2 - z := rfl
example : f = (fun x z => x + 1 + 2 - z) := rfl
example (x : Nat) : f x = fun z => x + 1 + 2 - z := rfl
example (y : Nat) : f (y := 5) = fun x z => x + 5 + 2 - z := rfl
def g {α} [Add α] (a : α) (b? : Option α := none) (c : α) : α :=
match b? with
| none => a + c
| some b => a + b + c
variable {α} [Add α]
example : g = fun (a c : α) => a + c := rfl
example (x : α) : g (c := x) = fun (a : α) => a + x := rfl
example (x : α) : g (b? := some x) = fun (a c : α) => a + x + c := rfl
example (x : α) : g x = fun (c : α) => x + c := rfl
example (x y : α) : g x y = fun (c : α) => x + y + c := rfl
In Lean 4, we can use .. to provide missing explicit arguments as _.
This feature combined with named arguments is useful for writing patterns. Here is an example:
inductive Term where
| var (name : String)
| num (val : Nat)
| add (fn : Term) (arg : Term)
| lambda (name : String) (type : Term) (body : Term)
def getBinderName : Term → Option String
| Term.lambda (name := n) .. => some n
| _ => none
def getBinderType : Term → Option Term
| Term.lambda (type := t) .. => some t
| _ => none
Ellipsis are also useful when explicit argument can be automatically inferred by Lean, and we want
to avoid a sequence of _s.
example (f : Nat → Nat) (a b c : Nat) : f (a + b + c) = f (a + (b + c)) :=
congrArg f (Nat.add_assoc ..)
In Lean 4, writing f(x) in place of f x is no longer allowed, you must use whitespace between the function and its arguments (e.g., f (x)).
Dependent function types
Given α : Type and β : α → Type, (x : α) → β x denotes the type of functions f with the property that,
for each a : α, f a is an element of β a. In other words, the type of the value returned by f depends on its input.
We say (x : α) → β x is a dependent function type. In Lean 3, we write the dependent function type (x : α) → β x using
one of the following three equivalent notations:
forall x : α, β x or ∀ x : α, β x or Π x : α, β x.
The first two were intended to be used for writing propositions, and the latter for writing code.
Although the notation Π x : α, β x has historical significance, we have removed it from Lean 4 because
it is awkward to use and often confuses new users. We can still write forall x : α, β x and ∀ x : α, β x.
#check forall (α : Type), α → α
#check ∀ (α : Type), α → α
#check ∀ α : Type, α → α
#check ∀ α, α → α
#check (α : Type) → α → α
#check {α : Type} → (a : Array α) → (i : Nat) → i < a.size → α
#check {α : Type} → [ToString α] → α → String
#check forall {α : Type} (a : Array α) (i : Nat), i < a.size → α
#check {α β : Type} → α → β → α × β
The meta keyword
In Lean 3, the keyword meta is used to mark definitions that can use primitives implemented in C/C++.
These metadefinitions can also call themselves recursively, relaxing the termination
restriction imposed by ordinary type theory. Metadefinitions may also use unsafe primitives such as
eval_expr (α : Type u) [reflected α] : expr → tactic α, or primitives that break referential transparency
tactic.unsafe_run_io.
The keyword meta has been currently removed from Lean 4. However, we may re-introduce it in the future,
but with a much more limited purpose: marking meta code that should not be included in the executables produced by Lean.
The keyword constant has been deleted in Lean 4, and axiom should be used instead. In Lean 4, the new command opaque is used to define an opaque definition. Here are two simple examples:
namespace meta1
opaque x : Nat := 1
-- The following example will not type check since `x` is opaque
-- example : x = 1 := rfl
-- We can evaluate `x`
#eval x
-- 1
-- When no value is provided, the elaborator tries to build one automatically for us
-- using the `Inhabited` type class
opaque y : Nat
end meta1
We can instruct Lean to use a foreign function as the implementation for any definition
using the attribute @[extern "foreign_function"]. It is the user's responsibility to ensure the
foreign implementation is correct.
However, a user mistake here will only impact the code generated by Lean, and
it will not compromise the logical soundness of the system.
That is, you cannot prove False using the @[extern] attribute.
We use @[extern] with definitions when we want to provide a reference implementation in Lean
that can be used for reasoning. When we write a definition such as
@[extern "lean_nat_add"]
def add : Nat → Nat → Nat
| a, Nat.zero => a
| a, Nat.succ b => Nat.succ (add a b)
Lean assumes that the foreign function lean_nat_add implements the reference implementation above.
The unsafe keyword allows us to define functions using unsafe features such as general recursion,
and arbitrary type casting. Regular (safe) functions cannot directly use unsafe ones since it would
compromise the logical soundness of the system. As in regular programming languages, programs written
using unsafe features may crash at runtime. Here are a few unsafe examples:
unsafe def unsound : False :=
unsound
#check @unsafeCast
-- {α : Type _} → {β : Type _} → α → β
unsafe def nat2String (x : Nat) : String :=
unsafeCast x
-- The following definition doesn't type check because it is not marked as `unsafe`
-- def nat2StringSafe (x : Nat) : String :=
-- unsafeCast x
The unsafe keyword is particularly useful when we want to take advantage of an implementation detail of the
Lean execution runtime. For example, we cannot prove in Lean that arrays have a maximum size, but
the runtime used to execute Lean programs guarantees that an array cannot have more than 2^64 (2^32) elements
in a 64-bit (32-bit) machine. We can take advantage of this fact to provide a more efficient implementation for
array functions. However, the efficient version would not be very useful if it can only be used in
unsafe code. Thus, Lean 4 provides the attribute @[implemented_by functionName]. The idea is to provide
an unsafe (and potentially more efficient) version of a safe definition or constant. The function f
at the attribute @[implemented_by f] is very similar to an extern/foreign function,
the key difference is that it is implemented in Lean itself. Again, the logical soundness of the system
cannot be compromised by using the attribute implemented_by, but if the implementation is incorrect your
program may crash at runtime. In the following example, we define withPtrUnsafe a k h which
executes k using the memory address where a is stored in memory. The argument h is proof
that k is a constant function. Then, we "seal" this unsafe implementation at withPtr. The proof h
ensures the reference implementation k 0 is correct. For more information, see the article
"Sealing Pointer-Based Optimizations Behind Pure Functions".
unsafe
def withPtrUnsafe {α β : Type} (a : α) (k : USize → β) (h : ∀ u, k u = k 0) : β :=
k (ptrAddrUnsafe a)
@[implemented_by withPtrUnsafe]
def withPtr {α β : Type} (a : α) (k : USize → β) (h : ∀ u, k u = k 0) : β :=
k 0
General recursion is very useful in practice, and it would be impossible to implement Lean 4 without it.
The keyword partial implements a very simple and efficient approach for supporting general recursion.
Simplicity was key here because of the bootstrapping problem. That is, we had to implement Lean in Lean before
many of its features were implemented (e.g., the tactic framework or support for wellfounded recursion).
Another requirement for us was performance. Functions tagged with partial should be as efficient as the ones implemented in mainstream functional programming
languages such as OCaml. When the partial keyword is used, Lean generates an auxiliary unsafe definition that
uses general recursion, and then defines an opaque constant that is implemented by this auxiliary definition.
This is very simple, efficient, and is sufficient for users that want to use Lean as a regular programming language.
A partial definition cannot use unsafe features such as unsafeCast and ptrAddrUnsafe, and it can only be used to
implement types we already known to be inhabited. Finally, since we "seal" the auxiliary definition using an opaque
constant, we cannot reason about partial definitions.
We are aware that proof assistants such as Isabelle provide a framework for defining partial functions that does not prevent users from proving properties about them. This kind of framework can be implemented in Lean 4. Actually, it can be implemented by users since Lean 4 is an extensible system. The developers current have no plans to implement this kind of support for Lean 4. However, we remark that users can implement it using a function that traverses the auxiliary unsafe definition generated by Lean, and produces a safe one using an approach similar to the one used in Isabelle.
namespace partial1
partial def f (x : Nat) : IO Unit := do
IO.println x
if x < 100 then
f (x+1)
#eval f 98
end partial1
Library changes
These are changes to the library which may trip up Lean 3 users:
Listis no longer a monad.
Style changes
Coding style changes have also been made:
- Term constants and variables are now
lowerCamelCaserather thansnake_case - Type constants are now
UpperCamelCase, egNat,List. Type variables are still lower case greek letters. Functors are still lower case latin(m : Type → Type) [Monad m]. - When defining typeclasses, prefer not to use "has". Eg
ToStringorAddinstead ofHasToStringorHasAdd. - Prefer
returntopurein monad expressions. - Pipes
<|are preferred to dollars$for function application. - Declaration bodies should always be indented:
inductive Hello where | foo | bar structure Point where x : Nat y : Nat def Point.addX : Point → Point → Nat := fun { x := a, .. } { x := b, .. } => a + b - In structures and typeclass definitions, prefer
whereto:=and don't surround fields with parentheses. (Shown inPointabove)
You can copy highlighted code straight from VS Code to any rich text editor supporting HTML input. For highlighting code in LaTeX, there are two options:
- listings, which is a common package and simple to set up, but you may run into some restrictions of it and LaTeX around Unicode
minted, a LaTeX package wrapping the Pygments syntax highlighting library. It needs a few more steps to set up, but provides unrestricted support for Unicode when combined with XeLaTeX or LuaLaTex.
Example with listings
Save lstlean.tex into the same directory, or anywhere in your TEXINPUTS path, as the following test file:
\documentclass{article}
\usepackage[T1]{fontenc}
\usepackage[utf8]{inputenc}
\usepackage{listings}
\usepackage{amssymb}
\usepackage{color}
\definecolor{keywordcolor}{rgb}{0.7, 0.1, 0.1} % red
\definecolor{tacticcolor}{rgb}{0.0, 0.1, 0.6} % blue
\definecolor{commentcolor}{rgb}{0.4, 0.4, 0.4} % grey
\definecolor{symbolcolor}{rgb}{0.0, 0.1, 0.6} % blue
\definecolor{sortcolor}{rgb}{0.1, 0.5, 0.1} % green
\definecolor{attributecolor}{rgb}{0.7, 0.1, 0.1} % red
\def\lstlanguagefiles{lstlean.tex}
% set default language
\lstset{language=lean}
\begin{document}
\begin{lstlisting}
theorem funext {f₁ f₂ : ∀ (x : α), β x} (h : ∀ x, f₁ x = f₂ x) : f₁ = f₂ := by
show extfunApp (Quotient.mk f₁) = extfunApp (Quotient.mk f₂)
apply congrArg
apply Quotient.sound
exact h
\end{lstlisting}
\end{document}
Compile the file via
$ pdflatex test.tex
- for older LaTeX versions, you might need to use
[utf8x]instead of[utf8]withinputenc
Example with minted
First install Pygments (version 2.18 or newer).
Then save the following sample LaTeX file test.tex into the same directory:
\documentclass{article}
\usepackage{fontspec}
% switch to a monospace font supporting more Unicode characters
\setmonofont{FreeMono}
\usepackage{minted}
\newmintinline[lean]{lean4}{bgcolor=white}
\newminted[leancode]{lean4}{fontsize=\footnotesize}
\usemintedstyle{tango} % a nice, colorful theme
\begin{document}
\begin{leancode}
theorem funext {f₁ f₂ : ∀ (x : α), β x} (h : ∀ x, f₁ x = f₂ x) : f₁ = f₂ := by
show extfunApp (Quotient.mk' f₁) = extfunApp (Quotient.mk' f₂)
apply congrArg
apply Quotient.sound
exact h
\end{leancode}
\end{document}
You can then compile test.tex by executing the following command:
xelatex --shell-escape test.tex
Some remarks:
- either
xelatexorlualatexis required to handle Unicode characters in the code. --shell-escapeis needed to allowxelatexto executepygmentizein a shell.- If the chosen monospace font is missing some Unicode symbols, you can direct them to be displayed using a fallback font or other replacement LaTeX code.
\usepackage{newunicodechar} \newfontfamily{\freeserif}{DejaVu Sans} \newunicodechar{✝}{\freeserif{✝}} \newunicodechar{𝓞}{\ensuremath{\mathcal{O}}} - If you are using an old version of Pygments, you can copy
lean.pyinto your working directory, and uselean4.py:Lean4Lexer -xinstead oflean4above. If your version ofmintedis v2.7 or newer, but before v3.0, you will additionally need to follow the workaround described in https://github.com/gpoore/minted/issues/360.
import Lean
open Lean Widget
The user-widgets system
Proving and programming are inherently interactive tasks. Lots of mathematical objects and data structures are visual in nature. User widgets let you associate custom interactive UIs with sections of a Lean document. User widgets are rendered in the Lean infoview.
Trying it out
To try it out, type in the following code and place your cursor over the #widget command.
You can also view this manual entry in the online editor.
@[widget_module]
def helloWidget: Widget.Module
helloWidget : Widget.Module: Type
Widget.Module where
javascript := "
import * as React from 'react';
export default function(props) {
const name = props.name || 'world'
return React.createElement('p', {}, 'Hello ' + name + '!')
}": String
"
import * as React from 'react';
export default function(props) {
const name = props.name || 'world'
return React.createElement('p', {}, 'Hello ' + name + '!')
}"
#widget helloWidget: Widget.Module
helloWidget
If you want to dive into a full sample right away, check out
Rubiks.
This sample uses higher-level widget components from the ProofWidgets library.
Below, we'll explain the system piece by piece.
⚠️ WARNING: All of the user widget APIs are unstable and subject to breaking changes.
Widget modules and instances
A widget module
is a valid JavaScript ESModule
that can execute in the Lean infoview.
Most widget modules export a React component
as the piece of user interface to be rendered.
To access React, the module can use import * as React from 'react'.
Our first example of a widget module is helloWidget above.
Widget modules must be registered with the @[widget_module] attribute.
A widget instance
is then the identifier of a widget module (e.g. `helloWidget)
bundled with a value for its props.
This value is passed as the argument to the React component.
In our first invocation of #widget, we set it to .null.
Try out what happens when you type in:
structure HelloWidgetProps: Type
HelloWidgetProps where
name?: HelloWidgetProps → Option String
name? : Option: Type → Type
Option String: Type
String := none: {α : Type} → Option α
none
deriving Server.RpcEncodable: Type → Type
Server.RpcEncodable
#widget helloWidget: Widget.Module
helloWidget with { name? := "<your name here>": String
"<your name here>" : HelloWidgetProps: Type
HelloWidgetProps }
Under the hood, widget instances are associated with a range of positions in the source file.
Widget instances are stored in the infotree
in the same manner as other information about the source file
such as the type of every expression.
In our example, the #widget command stores a widget instance
with the entire line as its range.
One can think of the infotree entry as an instruction for the infoview:
"when the user places their cursor here, please render the following widget".
Querying the Lean server
💡 NOTE: The RPC system presented below does not depend on JavaScript. However, the primary use case is the web-based infoview in VSCode.
Besides enabling us to create cool client-side visualizations,
user widgets have the ability to communicate with the Lean server.
Thanks to this, they have the same metaprogramming capabilities
as custom elaborators or the tactic framework.
To see this in action, let's implement a #check command as a web input form.
This example assumes some familiarity with React.
The first thing we'll need is to create an RPC method.
Meaning "Remote Procedure Call",this is a Lean function callable from widget code
(possibly remotely over the internet).
Our method will take in the name : Name of a constant in the environment and return its type.
By convention, we represent the input data as a structure.
Since it will be sent over from JavaScript,
we need FromJson and ToJson instance.
We'll see why the position field is needed later.
structure GetTypeParams: Type
GetTypeParams where
/-- Name of a constant to get the type of. -/
name: GetTypeParams → Name
name : Name: Type
Name
/-- Position of our widget instance in the Lean file. -/
pos: GetTypeParams → Lsp.Position
pos : Lsp.Position: Type
Lsp.Position
deriving FromJson: Type u → Type u
FromJson, ToJson: Type u → Type u
ToJson
After its argument structure, we define the getType method.
RPCs method execute in the RequestM monad and must return a RequestTask α
where α is the "actual" return type.
The Task is so that requests can be handled concurrently.
As a first guess, we'd use Expr as α.
However, expressions in general can be large objects
which depend on an Environment and LocalContext.
Thus we cannot directly serialize an Expr and send it to JavaScript.
Instead, there are two options:
- One is to send a reference which points to an object residing on the server. From JavaScript's point of view, references are entirely opaque, but they can be sent back to other RPC methods for further processing.
- The other is to pretty-print the expression and send its textual representation called
CodeWithInfos. This representation contains extra data which the infoview uses for interactivity. We take this strategy here.
RPC methods execute in the context of a file,
but not of any particular Environment,
so they don't know about the available definitions and theorems.
Thus, we need to pass in a position at which we want to use the local Environment.
This is why we store it in GetTypeParams.
The withWaitFindSnapAtPos method launches a concurrent computation
whose job is to find such an Environment for us,
in the form of a snap : Snapshot.
With this in hand, we can call MetaM procedures
to find out the type of name and pretty-print it.
open Server RequestM in
@[server_rpc_method]
def getType: GetTypeParams → RequestM (RequestTask CodeWithInfos)
getType (params: GetTypeParams
params : GetTypeParams: Type
GetTypeParams) : RequestM: Type → Type
RequestM (RequestTask: Type → Type
RequestTask CodeWithInfos: Type
CodeWithInfos) :=
withWaitFindSnapAtPos: {α : Type} → Lsp.Position → (Snapshots.Snapshot → RequestM α) → RequestM (RequestTask α)
withWaitFindSnapAtPos params: GetTypeParams
params.pos: GetTypeParams → Lsp.Position
pos fun snap: Snapshots.Snapshot
snap => do
runTermElabM: {α : Type} → Snapshots.Snapshot → RequestT Elab.TermElabM α → RequestM α
runTermElabM snap: Snapshots.Snapshot
snap do
let name: Name
name ← resolveGlobalConstNoOverloadCore: {m : Type → Type} → [Monad m] → [MonadResolveName m] → [MonadEnv m] → [MonadError m] → Name → m Name
resolveGlobalConstNoOverloadCore params: GetTypeParams
params.name: GetTypeParams → Name
name
let c: ConstantInfo
c ← try getConstInfo: {m : Type → Type} → [Monad m] → [MonadEnv m] → [MonadError m] → Name → m ConstantInfo
getConstInfo name: Name
name
catch _: Exception
_ => throwThe: (ε : Type) → {m : Type → Type} → [MonadExceptOf ε m] → {α : Type} → ε → m α
throwThe RequestError: Type
RequestError ⟨.invalidParams: JsonRpc.ErrorCode
.invalidParams, s!"no constant named '{name: Name
name}'"⟩
Widget.ppExprTagged: Expr → optParam PrettyPrinter.Delaborator.Delab PrettyPrinter.Delaborator.delab → MetaM CodeWithInfos
Widget.ppExprTagged c: ConstantInfo
c.type: ConstantInfo → Expr
type
Using infoview components
Now that we have all we need on the server side, let's write the widget module.
By importing @leanprover/infoview, widgets can render UI components used to implement the infoview itself.
For example, the <InteractiveCode> component displays expressions
with term : type tooltips as seen in the goal view.
We will use it to implement our custom #check display.
⚠️ WARNING: Like the other widget APIs, the infoview JS API is unstable and subject to breaking changes.
The code below demonstrates useful parts of the API.
To make RPC method calls, we invoke the useRpcSession hook.
The useAsync helper packs the results of an RPC call into an AsyncState structure
which indicates whether the call has resolved successfully,
has returned an error, or is still in-flight.
Based on this we either display an InteractiveCode component with the result,
mapRpcError the error in order to turn it into a readable message,
or show a Loading.. message, respectively.
@[widget_module]
def checkWidget: Widget.Module
checkWidget : Widget.Module: Type
Widget.Module where
javascript := "
import * as React from 'react';
const e = React.createElement;
import { useRpcSession, InteractiveCode, useAsync, mapRpcError } from '@leanprover/infoview';
export default function(props) {
const rs = useRpcSession()
const [name, setName] = React.useState('getType')
const st = useAsync(() =>
rs.call('getType', { name, pos: props.pos }), [name, rs, props.pos])
const type = st.state === 'resolved' ? st.value && e(InteractiveCode, {fmt: st.value})
: st.state === 'rejected' ? e('p', null, mapRpcError(st.error).message)
: e('p', null, 'Loading..')
const onChange = (event) => { setName(event.target.value) }
return e('div', null,
e('input', { value: name, onChange }), ' : ', type)
}
": String
"
import * as React from 'react';
const e = React.createElement;
import { useRpcSession, InteractiveCode, useAsync, mapRpcError } from '@leanprover/infoview';
export default function(props) {
const rs = useRpcSession()
const [name, setName] = React.useState('getType')
const st = useAsync(() =>
rs.call('getType', { name, pos: props.pos }), [name, rs, props.pos])
const type = st.state === 'resolved' ? st.value && e(InteractiveCode, {fmt: st.value})
: st.state === 'rejected' ? e('p', null, mapRpcError(st.error).message)
: e('p', null, 'Loading..')
const onChange = (event) => { setName(event.target.value) }
return e('div', null,
e('input', { value: name, onChange }), ' : ', type)
}
"
We can now try out the widget.
#widget checkWidget: Widget.Module
checkWidget

Building widget sources
While typing JavaScript inline is fine for a simple example,
for real developments we want to use packages from NPM, a proper build system, and JSX.
Thus, most actual widget sources are built with Lake and NPM.
They consist of multiple files and may import libraries which don't work as ESModules by default.
On the other hand a widget module must be a single, self-contained ESModule in the form of a string.
Readers familiar with web development may already have guessed that to obtain such a string, we need a bundler.
Two popular choices are rollup.js
and esbuild.
If we go with rollup.js, to make a widget work with the infoview we need to:
- Set
output.formatto'es'. - Externalize
react,react-dom,@leanprover/infoview. These libraries are already loaded by the infoview so they should not be bundled.
ProofWidgets provides a working rollup.js build configuration in
rollup.config.js.
Inserting text
Besides making RPC calls, widgets can instruct the editor to carry out certain actions.
We can insert text, copy text to the clipboard, or highlight a certain location in the document.
To do this, use the EditorContext React context.
This will return an EditorConnection
whose api field contains a number of methods that interact with the editor.
The full API can be viewed here.
@[widget_module]
def insertTextWidget: Widget.Module
insertTextWidget : Widget.Module: Type
Widget.Module where
javascript := "
import * as React from 'react';
const e = React.createElement;
import { EditorContext } from '@leanprover/infoview';
export default function(props) {
const editorConnection = React.useContext(EditorContext)
function onClick() {
editorConnection.api.insertText('-- hello!!!', 'above')
}
return e('div', null, e('button', { value: name, onClick }, 'insert'))
}
": String
"
import * as React from 'react';
const e = React.createElement;
import { EditorContext } from '@leanprover/infoview';
export default function(props) {
const editorConnection = React.useContext(EditorContext)
function onClick() {
editorConnection.api.insertText('-- hello!!!', 'above')
}
return e('div', null, e('button', { value: name, onClick }, 'insert'))
}
"
#widget insertTextWidget: Widget.Module
insertTextWidgetSemantic Highlighting
The Lean language server provides semantic highlighting information to editors. In order to benefit from this in VSCode, you may need to activate the "Editor > Semantic Highlighting" option in the preferences (this is translates to "editor.semanticHighlighting.enabled": true,
in settings.json). The default option here is to let your color theme decides whether it activates semantic highlighting (the default themes Dark+ and Light+ do activate it for instance).
However this may be insufficient if your color theme does not distinguish enough syntax categories or distinguishes them very subtly. For instance the default Light+ theme uses color #001080 for variables. This is awfully close to #000000 that is used as the default text color. This makes it very easy to miss an accidental use of auto bound implicit arguments. For instance in
def my_id (n : nat) := n
maybe nat is a typo and Nat was intended. If your color theme is good enough then you should see that n and nat have the same color since they are both marked as variables by semantic highlighting. If you rather write (n : Nat) then n keeps its variable color but Nat gets the default text color.
If you use such a bad theme, you can fix things by modifying the Semantic Token Color Customizations configuration. This cannot be done directly in the preferences dialog but you can click on "Edit in settings.json" to directly edit the settings file. Beware that you must save this file (in the same way you save any file opened in VSCode) before seeing any effect in other tabs or VSCode windows.
In the main config object, you can add something like
"editor.semanticTokenColorCustomizations": {
"[Default Light+]": {"rules": {"function": "#ff0000", "property": "#00ff00", "variable": "#ff00ff"}}
},
The colors in this example are not meant to be nice but to be easy to spot in your file when testing. Of course you need to replace Default Light+ with the name of your theme, and you can customize several themes if you use several themes. VSCode will display small colored boxes next to the HTML color specifications. Hovering on top of a color specification opens a convenient color picker dialog.
In order to understand what function, property and variable mean in the above example, the easiest path is to open a Lean file and ask VSCode about its classification of various bits of your file. Open the command palette with Ctrl-shift-p (or ⌘-shift-p on a Mac) and search for "Inspect Editor Tokens and Scopes" (typing the word "tokens" should be enough to see it). You can then click on any word in your file and look if there is a "semantic token type" line in the displayed information.
Development Workflow
If you want to make changes to Lean itself, start by building Lean from a clean checkout to make sure that everything is set up correctly. After that, read on below to find out how to set up your editor for changing the Lean source code, followed by further sections of the development manual where applicable such as on the test suite and commit convention.
If you are planning to make any changes that may affect the compilation of Lean itself, e.g. changes to the parser, elaborator, or compiler, you should first read about the bootstrapping pipeline.
You should not edit the stage0 directory except using the commands described in that section when necessary.
Development Setup
You can use any of the supported editors for editing the Lean source code.
If you set up elan as below, opening src/ as a workspace folder should ensure that stage 0 (i.e. the stage that first compiles src/) will be used for files in that directory.
Dev setup using elan
You can use elan to easily
switch between stages and build configurations based on the current
directory, both for the lean, leanc, and leanmake binaries in your shell's
PATH and inside your editor.
To install elan, you can do so, without installing a default version of Lean, using (Unix)
curl https://raw.githubusercontent.com/leanprover/elan/master/elan-init.sh -sSf | sh -s -- --default-toolchain none
or (Windows)
curl -O --location https://raw.githubusercontent.com/leanprover/elan/master/elan-init.ps1
powershell -f elan-init.ps1 --default-toolchain none
del elan-init.ps1
The lean-toolchain files in the Lean 4 repository are set up to use the lean4-stage0
toolchain for editing files in src and the lean4 toolchain for editing files in tests.
Run the following commands to make lean4 point at stage1 and lean4-stage0 point at stage0:
# in the Lean rootdir
elan toolchain link lean4 build/release/stage1
elan toolchain link lean4-stage0 build/release/stage0
You can also use the +toolchain shorthand (e.g. lean +lean4-debug) to switch
toolchains on the spot. lean4-mode will automatically use the lean executable
associated with the directory of the current file as long as lean4-rootdir is
unset and ~/.elan/bin is in your exec-path. Where Emacs sources the
exec-path from can be a bit unclear depending on your configuration, so
alternatively you can also set lean4-rootdir to "~/.elan" explicitly.
You might find that debugging through elan, e.g. via gdb lean, disables some
things like symbol autocompletion because at first only the elan proxy binary
is loaded. You can instead pass the explicit path to bin/lean in your build
folder to gdb, or use gdb $(elan which lean).
It is also possible to generate releases that others can use,
simply by pushing a tag to your fork of the Lean 4 github repository
(and waiting about an hour; check the Actions tab for completion).
If you push my-tag to a fork in your github account my_name,
you can then put my_name/lean4:my-tag in your lean-toolchain file in a project using lake.
(You must use a tag name that does not start with a numeral, or contain _).
VS Code
There is a lean.code-workspace file that correctly sets up VS Code with workspace roots for the stage0/stage1 setup described above as well as with other settings.
You should always load it when working on Lean, such as by invoking
code lean.code-workspace
on the command line.
ccache
Lean's build process uses ccache if it is
installed to speed up recompilation of the generated C code. Without
ccache, you'll likely spend more time than necessary waiting on
rebuilds - it's a good idea to make sure it's installed.
prelude
Unlike most Lean projects, all submodules of the Lean module begin with the
prelude keyword. This disables the automated import of Init, meaning that
developers need to figure out their own subset of Init to import. This is done
such that changing files in Init doesn't force a full rebuild of Lean.
Testing against Mathlib/Batteries
You can test a Lean PR against Mathlib and Batteries by rebasing your PR
on to nightly-with-mathlib branch. (It is fine to force push after rebasing.)
CI will generate a branch of Mathlib and Batteries called lean-pr-testing-NNNN
that uses the toolchain for your PR, and will report back to the Lean PR with results from Mathlib CI.
See https://leanprover-community.github.io/contribute/tags_and_branches.html for more details.
These are instructions to set up a working development environment for those who wish to make changes to Lean itself. It is part of the Development Guide.
We strongly suggest that new users instead follow the Quickstart to get started using Lean, since this sets up an environment that can automatically manage multiple Lean toolchain versions, which is necessary when working within the Lean ecosystem.
Requirements
- C++14 compatible compiler
- CMake
- GMP (GNU multiprecision library)
- LibUV
Platform-Specific Setup
- Linux (Ubuntu)
- Windows (msys2)
- Windows (WSL)
- macOS (homebrew)
- Linux/macOS/WSL via Nix: Call
nix developin the project root. That's it.
Generic Build Instructions
Setting up a basic parallelized release build:
git clone https://github.com/leanprover/lean4
cd lean4
cmake --preset release
make -C build/release -j$(nproc || sysctl -n hw.logicalcpu)
You can replace $(nproc || sysctl -n hw.logicalcpu) with the desired parallelism amount.
The above commands will compile the Lean library and binaries into the
stage1 subfolder; see below for details.
You should not usually run cmake --install after a successful build.
See Dev setup using elan on how to properly set up your editor to use the correct stage depending on the source directory.
Useful CMake Configuration Settings
Pass these along with the cmake --preset release command.
There are also two alternative presets that combine some of these options you can use instead of release: debug and sandebug (sanitize + debug).
-
-D CMAKE_BUILD_TYPE=
Select the build type. Valid values areRELEASE(default),DEBUG,RELWITHDEBINFO, andMINSIZEREL. -
-D CMAKE_C_COMPILER=
-D CMAKE_CXX_COMPILER=
Select the C/C++ compilers to use. Official Lean releases currently use Clang; see also.github/workflows/ci.ymlfor the CI config.
Lean will automatically use CCache if available to avoid redundant builds, especially after stage 0 has been updated.
Troubleshooting
- Call
makewith an additionalVERBOSE=1argument to print executed commands.
Installing Lean on Ubuntu
Build Dependencies
Please ensure you have the following build tools available and then follow the generic build instructions.
Basic packages
sudo apt-get install git libgmp-dev libuv1-dev cmake ccache clang pkgconf
Install Packages on OS X 14.5
We assume that you are using homebrew as a package manager.
Compilers
You need a C++11-compatible compiler to build Lean. As of November 2014, you have three options:
- clang++-3.5 (shipped with OSX, Apple LLVM version 6.0)
- gcc-4.9.1 (homebrew)
- clang++-3.5 (homebrew)
We recommend to use Apple's clang++ because it is pre-shipped with OS X and requires no further installation.
To install gcc-4.9.1 via homebrew, please execute:
brew install gcc
To install clang++-3.5 via homebrew, please execute:
brew install llvm
To use compilers other than the default one (Apple's clang++), you
need to use -DCMAKE_CXX_COMPILER option to specify the compiler
that you want to use when you run cmake. For example, do the
following to use g++.
cmake -DCMAKE_CXX_COMPILER=g++ ...
Required Packages: CMake, GMP, libuv, pkgconf
brew install cmake
brew install gmp
brew install libuv
brew install pkgconf
Recommended Packages: CCache
brew install ccache
Lean for Windows
A native Lean binary for Windows can be generated using MSYS2. It is easy to install all dependencies, it produces native 64/32-binaries, and supports a C++14 compiler.
An alternative to MSYS2 is to use Lean in Windows WSL.
While not necessary for pure building, you should first activate Developer Mode (Settings > Update & Security > For developers > Developer Mode), which will allow Lean to create symlinks that e.g. enable go-to-definition in the stdlib.
Installing the Windows SDK
Install the Windows SDK from Microsoft.
The oldest supported version is 10.0.18362.0. If you installed the Windows SDK to the default location,
then there should be a directory with the version number at C:\Program Files (x86)\Windows Kits\10\Include.
If there are multiple directories, only the highest version number matters.
Installing dependencies
The official webpage of MSYS2 provides one-click installers.
Once installed, you should run the "MSYS2 CLANG64" shell from the start menu (the one that runs clang64.exe).
Do not run "MSYS2 MSYS" or "MSYS2 MINGW64" instead!
MSYS2 has a package management system, pacman.
Here are the commands to install all dependencies needed to compile Lean on your machine.
pacman -S make python mingw-w64-clang-x86_64-cmake mingw-w64-clang-x86_64-clang mingw-w64-clang-x86_64-ccache mingw-w64-clang-x86_64-libuv mingw-w64-clang-x86_64-gmp git unzip diffutils binutils
You should now be able to run these commands:
clang --version
cmake --version
Then follow the generic build instructions in the MSYS2 MinGW shell, using:
cmake --preset release -DCMAKE_C_COMPILER=clang -DCMAKE_CXX_COMPILER=clang++
instead of cmake --preset release. This will use the clang compiler instead of gcc, which is required with msys2.
Install lean
Follow the steps in Dev setup using
elan regarding installation of the
bits you just built. Note that in an msys2 environment elan-init.sh
reports you need to add %USERPROFILE%\.elan\bin to your path, but of
course in msys2 that needs to be a valid linux style path, like this:
export PATH="$PATH:/c/users/$USERNAME/.elan/bin"
Running
You can run lean --version to see if your binaries work.
If you want a version that can run independently of your MSYS install then you need to copy the following dependent DLL's from where ever they are installed in your MSYS setup:
- libc++.dll
- libgmp-10.dll
- libuv-1.dll
- libwinpthread-1.dll
The following linux command will do that:
cp $(ldd lean.exe | cut -f3 -d' ' | grep mingw) .
However, if you plan to use this build to compile lean programs
to executable binaries using lake build in normal Windows command
prompt outside of msys2 environment you will also need to add a windows
version clang to your path.
Trouble shooting
-bash: gcc: command not found
Make sure /clang64/bin is in your PATH environment. If it is not then
check you launched the MSYS2 CLANG64 shell from the start menu.
(The one that runs clang64.exe).
Lean in Windows WSL
As an alternative to the MSYS2 setup you can also use the Windows Subsystem for Linux to build Lean there, but edit and debug using Visual Studio Code in Windows.
For the most part setup in WSL is the same as Ubuntu. This document provides additional information on how to setup Windows Visual Studio Code remote debugging into your WSL environment using the lean extension running in WSL.
It is recommended that you setup Ubuntu in WSL 2. Then follow the Dev setup using elan.
Visual Studio Code setup on Windows
Install Visual Studio Code on Windows. Install the VS Code
Remote Development extension from Microsoft. This extension
includes the Remote - WSL extension. Install the lean4 extension but
into the WSL using: Install in WSL: Ubuntu
Type Ctrl+Shift+P and select Remote-WSL: Open Folder in WSL... to
open a folder containing your hello world lean package.
When everything is working you should see something like this with a functioning infoview, syntax coloring and tooltips:
Troubleshooting
lean4: Could not find Lean version by running 'lean --version'.
Check that the lean program is available in your PATH in your WSL
environment.
Logs are showing up with a windows file path
Check that you have not set a windows path in your
lean4.serverLogging.path Visual Studio Code setting. it is best if
this setting is set as follows:
"lean4.serverLogging.path": "logs"
This will result in a logs folder being created inside your lean package folder in the WSL file system.
Lean Build Bootstrapping
Since version 4, Lean is a partially bootstrapped program: most parts of the frontend and compiler are written in Lean itself and thus need to be built before building Lean itself - which is needed to again build those parts. This cycle is broken by using pre-built C files checked into the repository (which ultimately go back to a point where the Lean compiler was not written in Lean) in place of these Lean inputs and then compiling everything in multiple stages up to a fixed point. The build directory is organized in these stages:
stage0/
# Bootstrap binary built from stage0/src/.
# We do not use any other files from this directory in further stages.
bin/lean
stage1/
include/
config.h # config variables used to build `lean` such as used allocator
runtime/lean.h # runtime header, used by extracted C code, uses `config.h`
share/lean/
lean.mk # used by `leanmake`
lib/
lean/**/*.olean # the Lean library (incl. the compiler) compiled by the previous stage's `lean`
temp/**/*.{c,o} # the library extracted to C and compiled by `leanc`
libInit.a libLean.a # static libraries of the Lean library
libleancpp.a # a static library of the C++ sources of Lean
libleanshared.so # a dynamic library including the static libraries above
bin/
lean # the Lean compiler & server, a small executable that calls directly into libleanshared.so
leanc # a wrapper around a C compiler supplying search paths etc
leanmake # a wrapper around `make` supplying the Makefile above
stage2/...
stage3/...
Stage 0 can be viewed as a blackbox since it does not depend on any local
changes and is equivalent to downloading a bootstrapping binary as done in other
compilers. The build for any other stage starts by building the runtime and
standard library from src/, using the lean binary from the previous stage in
the latter case, which are then assembled into a new bin/lean binary.
Each stage can be built by calling make stageN in the root build folder.
Running just make will default to stage 1, which is usually sufficient for
testing changes on the test suite or other files outside of the stdlib. However,
it might happen that the stage 1 compiler is not able to load its own stdlib,
e.g. when changing the .olean format: the stage 1 stdlib will use the format
generated by the stage 0 compiler, but the stage 1 compiler will expect the new
format. In this case, we should continue with building and testing stage 2
instead, which will both build and expect the new format. Note that this is only
possible because when building a stage's stdlib, we use the previous compiler
but never load the previous stdlib (since everything is prelude). We can also
use stage 2 to test changes in the compiler or other "meta" parts, i.e. changes
that affect the produced (.olean or .c) code, on the stdlib and compiler itself.
We are not aware of any "meta-meta" parts that influence more than two stages of
compilation, so stage 3 should always be identical to stage 2 and only exists as
a sanity check.
In summary, doing a standard build via make internally involves these steps:
- compile the
stage0/srcarchived sources intostage0/bin/lean - use it to compile the current library (including your changes) into
stage1/lib - link that and the current C++ code from
src/intostage1/bin/lean
You now have a Lean binary and library that include your changes, though their own compilation was not influenced by them, that you can use to test your changes on test programs whose compilation will be influenced by the changes.
Updating stage0
Finally, when we want to use new language features in the library, we need to
update the archived C source code of the stage 0 compiler in stage0/src.
The github repository will automatically update stage0 on master once
src/stdlib_flags.h and stage0/src/stdlib_flags.h are out of sync.
If you have write access to the lean4 repository, you can also manually trigger that process, for example to be able to use new features in the compiler itself. You can do that on https://github.com/leanprover/lean4/actions/workflows/update-stage0.yml or using Github CLI with
gh workflow run update-stage0.yml
Leaving stage0 updates to the CI automation is preferable, but should you need
to do it locally, you can use make update-stage0-commit in build/release to
update stage0 from stage1 or make -C stageN update-stage0-commit to
update from another stage. This command will automatically stage the updated files
and introduce a commit,so make sure to commit your work before that.
If you rebased the branch (either onto a newer version of master, or fixing
up some commits prior to the stage0 update, recreate the stage0 update commits.
The script script/rebase-stage0.sh can be used for that.
The CI should prevent PRs with changes to stage0 (besides stdlib_flags.h)
from entering master through the (squashing!) merge queue, and label such PRs
with the changes-stage0 label. Such PRs should have a cleaned up history,
with separate stage0 update commits; then coordinate with the admins to merge
your PR using rebase merge, bypassing the merge queue.
Further Bootstrapping Complications
As written above, changes in meta code in the current stage usually will only affect later stages. This is an issue in two specific cases.
-
For the special case of quotations, it is desirable to have changes in builtin parsers affect them immediately: when the changes in the parser become active in the next stage, builtin macros implemented via quotations should generate syntax trees compatible with the new parser, and quotation patterns in builtin macros and elaborators should be able to match syntax created by the new parser and macros. Since quotations capture the syntax tree structure during execution of the current stage and turn it into code for the next stage, we need to run the current stage's builtin parsers in quotations via the interpreter for this to work. Caveats:
- We activate this behavior by default when building stage 1 by setting
-Dinternal.parseQuotWithCurrentStage=true. We force-disable it insidemacro/macro_rules/elab/elab_rulesviasuppressInsideQuotas they are guaranteed not to run in the next stage and may need to be run in the current one, so the stage 0 parser is the correct one to use for them. It may be necessary to extend this disabling to functions that contain quotations and are (exclusively) used by one of the mentioned commands. A function using quotations should never be used by both builtin and non-builtin macros/elaborators. Example: https://github.com/leanprover/lean4/blob/f70b7e5722da6101572869d87832494e2f8534b7/src/Lean/Elab/Tactic/Config.lean#L118-L122 - The parser needs to be reachable via an
importstatement, otherwise the version of the previous stage will silently be used. - Only the parser code (
Parser.fn) is affected; all metadata such as leading tokens is taken from the previous stage.
For an example, see https://github.com/leanprover/lean4/commit/f9dcbbddc48ccab22c7674ba20c5f409823b4cc1#diff-371387aed38bb02bf7761084fd9460e4168ae16d1ffe5de041b47d3ad2d22422R13
- We activate this behavior by default when building stage 1 by setting
-
For non-builtin meta code such as
notations ormacros inNotation.lean, we expect changes to affect the current file and all later files of the same stage immediately, just like outside the stdlib. To ensure this, we build stage 1 using-Dinterpreter.prefer_native=false- otherwise, when executing a macro, the interpreter would notice that there is already a native symbol available for this function and run it instead of the new IR, but the symbol is from the previous stage!To make matters more complicated, while
falseis a reasonable default incurring only minor overhead (ParserDescrs and simple macros are cheap to interpret), there are situations where we need to set the option totrue: when the interpreter is executed from the native code of the previous stage, the type of the value it computes must be identical to/ABI-compatible with the type in the previous stage. For example, if we add a new parameter toMacroor reorder constructors inParserDescr, building the stage with the interpreter will likely fail. Thus we need to setinterpreter.prefer_nativetotruein such cases to "freeze" meta code at their versions in the previous stage; no new meta code should be introduced in this stage. Any further stages (e.g. after anupdate-stage0) will then need to be compiled with the flag set tofalseagain since they will expect the new signature.When enabling
prefer_native, we usually want to disableparseQuotWithCurrentStageas it would otherwise make quotations use the interpreter after all. However, there is a specific case where we want to set both options totrue: when we make changes to a non-builtin parser likesimpthat has a builtin elaborator, we cannot have the new parser be active outside of quotations in stage 1 as the builtin elaborator from stage 0 would not understand them; on the other hand, we need quotations in e.g. the builtinsimpelaborator to produce the new syntax in the next stage. As this issue usually affects only tactics, enablingdebug.byAsSorryinstead ofprefer_nativecan be a simpler solution.For a
prefer_nativeexample, see https://github.com/leanprover/lean4/commit/da4c46370d85add64ef7ca5e7cc4638b62823fbb.
To modify either of these flags both for building and editing the stdlib, adjust
the code in stage0/src/stdlib_flags.h. The flags will automatically be reset
on the next update-stage0 when the file is overwritten with the original
version in src/.
Test Suite
After building Lean you can run all the tests using
cd build/release
make test ARGS=-j4
Change the 4 to the maximum number of parallel tests you want to
allow. The best choice is the number of CPU cores on your machine as
the tests are mostly CPU bound. You can find the number of processors
on linux using nproc and on Windows it is the NUMBER_OF_PROCESSORS
environment variable.
You can run tests after building a specific stage by
adding the -C stageN argument. The default when run as above is stage 1. The
Lean tests will automatically use that stage's corresponding Lean
executables
Running make test will not pick up new test files; run
cmake build/release/stage1
to update the list of tests.
You can also use ctest directly if you are in the right folder. So
to run stage1 tests with a 300 second timeout run this:
cd build/release/stage1
ctest -j 4 --output-on-failure --timeout 300
Useful ctest flags are -R <name of test> to run a single test, and
--rerun-failed to run all tests that failed during the last run.
You can also pass ctest flags via make test ARGS="--rerun-failed".
To get verbose output from ctest pass the --verbose command line
option. Test output is normally suppressed and only summary
information is displayed. This option will show all test output.
Test Suite Organization
All these tests are included by src/shell/CMakeLists.txt:
-
tests/lean: contains tests that come equipped with a .lean.expected.out file. The driver scripttest_single.shruns each test and checks the actual output (*.produced.out) with the checked in expected output. -
tests/lean/run: contains tests that are run through the lean command line one file at a time. These tests only look for error codes and do not check the expected output even though output is produced, it is ignored. -
tests/lean/interactive: are designed to test server requests at a given position in the input file. Each .lean file contains comments that indicate how to simulate a client request at that position. using a--^point to the line position. Example:open Foo in theorem tst2 (h : a ≤ b) : a + 2 ≤ b + 2 := Bla. --^ textDocument/completionIn this example, the test driver
test_single.shwill simulate an auto-completion request atBla.. The expected output is stored in a .lean.expected.out in the json format that is part of the Language Server Protocol.This can also be used to test the following additional requests:
--^ textDocument/hover --^ textDocument/typeDefinition --^ textDocument/definition --^ $/lean/plainGoal --^ $/lean/plainTermGoal --^ insert: ... --^ collectDiagnostics -
tests/lean/server: Tests more of the Lean--serverprotocol. There are just a few of them, and it uses .log files containing JSON. -
tests/compiler: contains tests that will run the Lean compiler and build an executable that is executed and the output is compared to the .lean.expected.out file. This test also contains a subfolderforeignwhich shows how to extend Lean using C++. -
tests/lean/trust0: tests that run Lean in a mode that Lean doesn't even trust the .olean files (i.e., trust 0). -
tests/bench: contains performance tests. -
tests/plugin: tests that compiled Lean code can be loaded intoleanvia the--plugincommand line option.
Writing Good Tests
Every test file should contain:
- an initial
/-! -/module docstring summarizing the test's purpose - a module docstring for each test section that describes what is tested and, if not 100% clear, why that is the desirable behavior
At the time of writing, most tests do not follow these new guidelines yet.
For an example of a conforming test, see tests/lean/1971.lean.
Fixing Tests
When the Lean source code or the standard library are modified, some of the
tests break because the produced output is slightly different, and we have
to reflect the changes in the .lean.expected.out files.
We should not blindly copy the new produced output since we may accidentally
miss a bug introduced by recent changes.
The test suite contains commands that allow us to see what changed in a convenient way.
First, we must install meld. On Ubuntu, we can do it by simply executing
sudo apt-get install meld
Now, suppose bad_class.lean test is broken. We can see the problem by going to tests/lean directory and
executing
./test_single.sh -i bad_class.lean
When the -i option is provided, meld is automatically invoked
whenever there is discrepancy between the produced and expected
outputs. meld can also be used to repair the problems.
In Emacs, we can also execute M-x lean4-diff-test-file to check/diff the file of the current buffer.
To mass-copy all .produced.out files to the respective .expected.out file, use tests/lean/copy-produced.
Debugging
Some notes on how to debug Lean, which may also be applicable to debugging Lean programs in general.
Tracing
In CoreM and derived monads, we use trace[traceCls] "msg with {interpolations}" to fill the structured trace viewable with set_option trace.traceCls true.
New trace classes have to be registered using registerTraceClass first.
Notable trace classes:
-
Elab.command/Elab.step: command/term macro expansion/elaboration stepsUseful options modifying these traces for debugging syntax trees:
set_option pp.raw true set_option pp.raw.maxDepth 10 -
Meta.synthInstance: typeclass resolution -
Meta.isDefEq: unification -
interpreter: full execution trace of the interpreter. Only available in debug builds.
In pure contexts or when execution is aborted before the messages are finally printed, one can instead use the term dbg_trace "msg with {interpolations}"; val (; can also be replaced by a newline), which will print the message to stderr before evaluating val. dbgTraceVal val can be used as a shorthand for dbg_trace "{val}"; val.
Note that if the return value is not actually used, the trace code is silently dropped as well.
By default, such stderr output is buffered and shown as messages after a command has been elaborated, which is necessary to ensure deterministic ordering of messages under parallelism.
If Lean aborts the process before it can finish the command or takes too long to do that, using -DstderrAsMessages=false avoids this buffering and shows dbg_trace output (but not traces or other diagnostics) immediately.
Debuggers
gdb/lldb can be used to inspect stack traces of compiled Lean code, though they cannot print values of Lean variables and terms in any legible way yet.
For example, b lean_panic_fn can be used to look at the stack trace of a panic.
The rr reverse debugger is an amazing tool for investigating e.g. segfaults from reference counting errors, though better hope you will never need it...
Git Commit Convention
We are using the following convention for writing git commit messages. For pull requests, make sure the pull request title and description follow this convention, as the squash-merge commit will inherit title and body from the pull request.
This convention is based on the one from the AngularJS project (doc, commits).
Format of the commit message
<type>: <subject>
<NEWLINE>
<body>
<NEWLINE>
<footer>
<type> is:
- feat (feature)
- fix (bug fix)
- doc (documentation)
- style (formatting, missing semicolons, ...)
- refactor
- test (when adding missing tests)
- chore (maintain, ex: travis-ci)
- perf (performance improvement, optimization, ...)
Every feat or fix commit must have a changelog-* label, and a commit message
beginning with "This PR " that will be included in the changelog.
<subject> has the following constraints:
- use imperative, present tense: "change" not "changed" nor "changes"
- do not capitalize the first letter
- no dot(.) at the end
<body> has the following constraints:
- just as in
<subject>, use imperative, present tense - includes motivation for the change and contrasts with previous behavior
- If a
changelog-*label is present, the body must begin with "This PR ".
<footer> is optional and may contain two items:
-
Breaking changes: All breaking changes have to be mentioned in footer with the description of the change, justification and migration notes
-
Referencing issues: Closed bugs should be listed on a separate line in the footer prefixed with "Closes" keyword like this:
Closes #123, #456
Examples
fix: add declarations for operator<<(std::ostream&, expr const&) and operator<<(std::ostream&, context const&) in the kernel
This PR adds declarations operator<< for raw printing.
The actual implementation of these two operators is outside of the
kernel. They are implemented in the file 'library/printer.cpp'.
We declare them in the kernel to prevent the following problem. Suppose there is a file 'foo.cpp' that does not include 'library/printer.h', but contains
expr a;
...
std::cout << a << "\n";
...
The compiler does not generate an error message. It silently uses the operator bool() to coerce the expression into a Boolean. This produces counter-intuitive behavior, and may confuse developers.
Releasing a stable version
This checklist walks you through releasing a stable version. See below for the checklist for release candidates.
We'll use v4.6.0 as the intended release version as a running example.
- Run
script/release_checklist.py v4.6.0to check the status of the release. This script is idempotent, and should be safe to run at any stage of the release process. Note that as of v4.19.0, this script takes some autonomous actions, which can be prevented via--dry-run. git checkout releases/v4.6.0(This branch should already exist, from the release candidates.)git pull- In
src/CMakeLists.txt, verify you seeset(LEAN_VERSION_MINOR 6)(for whichever6is appropriate)set(LEAN_VERSION_IS_RELEASE 1)- (all of these should already be in place from the release candidates)
git tag v4.6.0git push $REMOTE v4.6.0, where$REMOTEis the upstream Lean repository (e.g.,origin,upstream)- Now wait, while CI runs.
- You can monitor this at
https://github.com/leanprover/lean4/actions/workflows/ci.yml, looking for thev4.6.0tag. - This step can take up to two hours.
- If you are intending to cut the next release candidate on the same day, you may want to start on the release candidate checklist now.
- You can monitor this at
- Next we need to prepare the release notes.
- If the stable release is identical to the last release candidate (this should usually be the case), you can reuse the release notes that are already in the Lean Language Reference.
- If you want to regenerate the release notes,
run
script/release_notes.py --since v4.5.0on thereleases/v4.6.0branch, and see the section "Writing the release notes" below for more information. - Release notes live in https://github.com/leanprover/reference-manual, in e.g.
Manual/Releases/v4.6.0.lean. It's best if you update these at the same time as a you update thelean-toolchainfor thereference-manualrepository, see below.
- Go to https://github.com/leanprover/lean4/releases and verify that the
v4.6.0release appears.- Verify on Github that "Set as the latest release" is checked.
- Next, we will move a curated list of downstream repos to the latest stable release.
- In order to have the access rights to push to these repositories and merge PRs,
you will need to be a member of the
lean-release-managersteam at bothleanprover-communityandleanprover. Contact Kim Morrison (@kim-em) to arrange access. - For each of the repositories listed in
script/release_repos.yml,- Run
script/release_steps.py v4.6.0 <repo>(e.g. replacing<repo>withbatteries), which will walk you through the following steps:- Create a new branch off
master/main(as specified in thebranchfield), calledbump_to_v4.6.0. - Update the contents of
lean-toolchaintoleanprover/lean4:v4.6.0. - In the
lakefile.tomlorlakefile.lean, if there are dependencies on specific version tags of dependencies, update them to the new tag. If they depend onmainormaster, don't change this; you've just updated the dependency, solake updatewill take care of modifying the manifest. - Run
lake update - Commit the changes as
chore: bump toolchain to v4.6.0and push. - Create a PR with title "chore: bump toolchain to v4.6.0".
- Create a new branch off
- Merge the PR once CI completes.
- Re-running
script/release_checklist.pywill then create the tagv4.6.0frommaster/mainand push it (unlesstoolchain-tag: falsein therelease_repos.ymlfile) script/release_checklist.pywill then merge the tagv4.6.0into thestablebranch and push it (unlessstable-branch: falsein therelease_repos.ymlfile).
- Run
- Special notes on repositories with exceptional requirements:
doc-gen4has addition dependencies which we do not update at each toolchain release, although occasionally these break and need to be updated manually.verso:- The
subversodependency is unusual in that it needs to be compatible with every Lean release simultaneously. Usually you don't need to do anything. If you think something is wrong here please contact David Thrane Christiansen (@david-christiansen) - Warnings during
lake updateandlake buildare expected.
- The
reference-manual: the release notes generated byscript/release_notes.pyas described above must be included inManual/Releases/v4.6.0.lean, andimportandincludestatements adding inManual/Releases.lean.ProofWidgets4uses a non-standard sequential version tagging scheme, e.g.v0.0.29, which does not refer to the toolchain being used. You will need to identify the next available version number from https://github.com/leanprover-community/ProofWidgets4/releases, and push a new tag after merging the PR tomain.mathlib4:- The
lakefile.tomlshould always refer to dependencies via theirmainormasterbranch, not a toolchain tag (with the exception ofProofWidgets4, which must use a sequential version tag). - Push the PR branch to the main Mathlib repository rather than a fork, or CI may not work reliably
- The
repl: There are two copies oflean-toolchain/lakefile.lean: in the root, and intest/Mathlib/. Edit both, and runlake updatein both directories.
- In order to have the access rights to push to these repositories and merge PRs,
you will need to be a member of the
- An awkward situtation that sometimes occurs (e.g. with Verso) is that the
master/mainbranch has already been moved to a nightly toolchain that comes after the stable toolchain we are targeting. In this case it is necessary to create a branchreleases/v4.6.0from the last commit which was on an earlier toolchain, move that branch to the stable toolchain, and create the toolchain tag from that branch. - Run
script/release_checklist.py v4.6.0one last time to check that everything is in order. - Finally, make an announcement!
This should go in https://leanprover.zulipchat.com/#narrow/stream/113486-announce, with topic
v4.6.0. Please see previous announcements for suggested language. You will want a few bullet points for main topics from the release notes. If there is a blog post, link to that from the zulip announcement. - Make sure that whoever is handling social media knows the release is out.
Time estimates:
- Initial checks and push the tag: 10 minutes.
- Waiting for the release: 120 minutes.
- Preparing release notes: 10 minutes.
- Bumping toolchains in downstream repositories, up to creating the Mathlib PR: 60 minutes.
- Waiting for Mathlib CI and bors: 120 minutes.
- Finalizing Mathlib tags and stable branch, and updating REPL: 20 minutes.
- Posting announcement and/or blog post: 30 minutes.
Creating a release candidate.
This checklist walks you through creating the first release candidate for a version of Lean.
We'll use v4.7.0-rc1 as the intended release version in this example.
- Decide which nightly release you want to turn into a release candidate.
We will use
nightly-2024-02-29in this example. - It is essential to choose the nightly that will become the release candidate as early as possible, to avoid confusion.
- Throughout this process you can use
script/release_checklist.py v4.7.0-rc1to track progress. This script will also try to do some steps autonomously. It is idempotent and safe to run at any point. You can prevent it taking any actions using--dry-run. - It is essential that Batteries and Mathlib already have reviewed branches compatible with this nightly.
- Check that both Batteries and Mathlib's
bump/v4.7.0branch containnightly-2024-02-29in theirlean-toolchain. - The steps required to reach that state are beyond the scope of this checklist, but see below!
- Check that both Batteries and Mathlib's
- Create the release branch from this nightly tag:
git remote add nightly https://github.com/leanprover/lean4-nightly.git git fetch nightly tag nightly-2024-02-29 git checkout nightly-2024-02-29 git checkout -b releases/v4.7.0 git push --set-upstream origin releases/v4.18.0 - In
src/CMakeLists.txt,- verify that you see
set(LEAN_VERSION_MINOR 7)(for whichever7is appropriate); this should already have been updated when the development cycle began. - change the
LEAN_VERSION_IS_RELEASEline toset(LEAN_VERSION_IS_RELEASE 1)(this should be a change; onmasterand nightly releases it is always0). - Commit your changes to
src/CMakeLists.txt, and push.
- verify that you see
git tag v4.7.0-rc1git push origin v4.7.0-rc1- Now wait, while CI runs.
- The CI setup parses the tag to discover the
-rc1special description, and passes it tocmakeusing a-Doption. The-rc1doesn't need to be placed in the configuration file. - You can monitor this at
https://github.com/leanprover/lean4/actions/workflows/ci.yml, looking for thev4.7.0-rc1tag. - This step can take up to two hours.
- The CI setup parses the tag to discover the
- Verify that the release appears at https://github.com/leanprover/lean4/releases/, marked as a prerelease (this should have been done automatically by the CI release job).
- Next we need to prepare the release notes.
- Run
script/release_notes.py --since v4.6.0on thereleases/v4.7.0branch, which will report diagnostic messages onstderr(including reporting commits that it couldn't associate with a PR, and hence will be omitted) and then a chunk of markdown onstdout. See the section "Writing the release notes" below for more information. - Release notes live in https://github.com/leanprover/reference-manual, in e.g.
Manual/Releases/v4.7.0.lean. It's best if you update these at the same time as a you update thelean-toolchainfor thereference-manualrepository, see below.
- Run
- Next, we will move a curated list of downstream repos to the release candidate.
- This assumes that for each repository either:
- There is already a reviewed branch
bump/v4.7.0containing the required adaptations. The preparation of this branch is beyond the scope of this document. - The repository does not need any changes to move to the new version.
- Note that sometimes there are unreviewed but necessary changes on the
nightly-testingbranch of the repository. If so, you will need to merge these into thebump_to_v4.7.0-rc1branch manually.
- There is already a reviewed branch
- For each of the repositories listed in
script/release_repos.yml,- Run
script/release_steps.py v4.7.0-rc1 <repo>(e.g. replacing<repo>withbatteries), which will walk you through the following steps:- Create a new branch off
master/main(as specified in thebranchfield), calledbump_to_v4.7.0-rc1. - Merge
origin/bump/v4.7.0if relevant (i.e.bump-branch: trueappears inrelease_repos.yml). - Update the contents of
lean-toolchaintoleanprover/lean4:v4.7.0-rc1. - In the
lakefile.tomlorlakefile.lean, if there are dependencies onnightly-testing,bump/v4.7.0, or specific version tags, update them to the new tag. If they depend onmainormaster, don't change this; you've just updated the dependency, solake updatewill take care of modifying the manifest. - Run
lake update - Run
lake build && if lake check-test; then lake test; fito check things are working. - Commit the changes as
chore: bump toolchain to v4.7.0-rc1and push. - Create a PR with title "chore: bump toolchain to v4.7.0-rc1".
- Create a new branch off
- Merge the PR once CI completes.
- Re-running
script/release_checklist.pywill then create the tagv4.7.0-rc1frommaster/mainand push it (unlesstoolchain-tag: falsein therelease_repos.ymlfile)
- Run
- We do this for the same list of repositories as for stable releases, see above for notes about special cases.
As above, there are dependencies between these, and so the process above is iterative.
It greatly helps if you can merge the
bump/v4.7.0PRs yourself! - It is essential for Mathlib and Batteries CI that you then create the next
bump/v4.8.0branch for the next development cycle. Set thelean-toolchainfile on this branch to samenightlyyou used for this release.
- This assumes that for each repository either:
- Run
script/release_checklist.py v4.7.0-rc1one last time to check that everything is in order. - Make an announcement!
This should go in https://leanprover.zulipchat.com/#narrow/stream/113486-announce, with topic
v4.7.0-rc1. Please see previous announcements for suggested language. You will want a few bullet points for main topics from the release notes. Please also make sure that whoever is handling social media knows the release is out. - Begin the next development cycle (i.e. for
v4.8.0) on the Lean repository, by making a PR that:- Uses branch name
dev_cycle_v4.8. - Updates
src/CMakeLists.txtto sayset(LEAN_VERSION_MINOR 8) - Titled "chore: begin development cycle for v4.8.0"
- Uses branch name
Time estimates:
Slightly longer than the corresponding steps for a stable release.
Similar process, but more things go wrong.
In particular, updating the downstream repositories is significantly more work
(because we need to merge existing bump/v4.7.0 branches, not just update a toolchain).
Preparing bump/v4.7.0 branches
While not part of the release process per se, this is a brief summary of the work that goes into updating Batteries/Aesop/Mathlib to new versions.
Please read https://leanprover-community.github.io/contribute/tags_and_branches.html
- Each repo has an unreviewed
nightly-testingbranch that receives commits automatically frommaster, and has its toolchain updated automatically for every nightly. (Note: the aesop branch is not automated, and is updated on an as needed basis.) As a consequence this branch is often broken. A bot posts in the (private!) "Mathlib reviewers" stream on Zulip about the status of these branches. - We fix the breakages by committing directly to
nightly-testing: there is no PR process.- This can either be done by the person managing this process directly, or by soliciting assistance from authors of files, or generally helpful people on Zulip!
- Each repo has a
bump/v4.7.0which accumulates reviewed changes adapting to new versions. - Once
nightly-testingis working on a given nightly, saynightly-2024-02-15, we will create a PR tobump/v4.7.0. - For Mathlib, there is a script in
scripts/create-adaptation-pr.shthat automates this process. - For Batteries and Aesop it is currently manual.
- For all of these repositories, the process is the same:
- Make sure
bump/v4.7.0is up to date withmaster(by mergingmaster, no PR necessary) - Create from
bump/v4.7.0abump/nightly-2024-02-15branch. - In that branch,
git merge nightly-testingto bring across changes fromnightly-testing. - Sanity check changes, commit, and make a PR to
bump/v4.7.0from thebump/nightly-2024-02-15branch. - Solicit review, merge the PR into
bump/v4.7.0.
- Make sure
- It is always okay to merge in the following directions:
master->bump/v4.7.0->bump/nightly-2024-02-15->nightly-testing. Please remember to push any merges you make to intermediate steps!
Writing the release notes
Release notes are automatically generated from the commit history, using script/release_notes.py.
Run this as script/release_notes.py --since v4.6.0, where v4.6.0 is the previous release version.
This script should be run on the releases/v4.7.0 branch.
This will generate output for all commits since that tag.
Note that there is output on both stderr, which should be manually reviewed,
and on stdout, which should be manually copied into the reference-manual repository, in the file Manual/Releases/v4.7.0.lean.
The output on stderr should mostly be about commits for which the script could not find an associated PR, usually because a PR was rebase-merged because it contained an update to stage0. Some judgement is required here: ignore commits which look minor, but manually add items to the release notes for significant PRs that were rebase-merged.
There can also be pre-written entries in ./releases_drafts, which should be all incorporated in the release notes and then deleted from the branch.
See ./releases_drafts/README.md for more information.
Documentation
The Lean doc folder contains the Lean Manual and is
authored in a combination of markdown (*.md) files and literate Lean files. The .lean files are
preprocessed using a tool called LeanInk and
Alectryon which produces a generated markdown file. We then run
mdbook on the result to generate the html pages.
Settings
We are using the following settings while editing the markdown docs.
{
"files.insertFinalNewline": true,
"files.trimTrailingWhitespace": true,
"[markdown]": {
"rewrap.wrappingColumn": 70
}
}
Build
Using Nix
Building the manual using Nix (which is what the CI does) is as easy as
$ nix build --update-input lean ./doc
You can also open a shell with mdbook for running the commands mentioned below with
nix develop ./doc#book. Otherwise, read on.
Manually
To build and test the book you have to preprocess the .lean files with Alectryon then use our own fork of the Rust tool named mdbook. We have our own fork of mdBook with the following additional features:
- Add support for hiding lines in other languages #1339
- Make
mdbook testcall theleancompiler to test the snippets. - Ability to test a single chapter at a time which is handy when you
are working on that chapter. See the
--chapteroption.
So you need to setup these tools before you can run mdBook.
-
install Rust which provides you with the
cargotool for building rust packages. Then run the following:cargo install --git https://github.com/leanprover/mdBook mdbook -
Clone https://github.com/leanprover/LeanInk.git and run
lake buildthen make the resulting binary available to Alectryon using e.g.# make `leanInk` available in the current shell export PATH=$PWD/build/bin:$PATH -
Create a Python 3.10 environment.
-
Install Alectryon:
python3 -m pip install git+https://github.com/Kha/alectryon.git@typeid -
Now you are ready to process the
*.leanfiles using Alectryon as follows:cd lean4/doc alectryon --frontend lean4+markup examples/palindromes.lean --backend webpage -o palindromes.lean.mdRepeat this for the other .lean files you care about or write a script to process them all.
-
Now you can build the book using:
cd lean4/doc mdbook build
This will put the HTML in a out folder so you can load out/index.html in your web browser and
it should look like https://lean-lang.org/lean4/doc/.
-
It is also handy to use e.g.
mdbook watchin thedoc/folder so that it keeps the html up to date while you are editing.mdbook watch --open # opens the output in `out/` in your default browser
Testing Lean Snippets
You can run the following in the doc/ folder to test all the lean code snippets.
```bash
mdbook test
```
and you can use the --chapter option to test a specific chapter that you are working on:
```bash
mdbook test --chapter Array
```
Use chapter name ? to get a list of all the chapter names.
Foreign Function Interface
NOTE: The current interface was designed for internal use in Lean and should be considered unstable. It will be refined and extended in the future.
As Lean is written partially in Lean itself and partially in C++, it offers efficient interoperability between the two languages (or rather, between Lean and any language supporting C interfaces).
This support is however currently limited to transferring Lean data types; in particular, it is not possible yet to pass or return compound data structures such as C structs by value from or to Lean.
There are two primary attributes for interoperating with other languages:
@[extern "sym"] constant leanSym : ...binds a Lean declaration to the external symbolsym. It can also be used withdefto provide an internal definition, but ensuring consistency of both definitions is up to the user.@[export sym] def leanSym : ...exportsleanSymunder the unmangled symbol namesym.
For simple examples of how to call foreign code from Lean and vice versa, see https://github.com/leanprover/lean4/blob/master/src/lake/examples/ffi and https://github.com/leanprover/lean4/blob/master/src/lake/examples/reverse-ffi, respectively.
The Lean ABI
The Lean Application Binary Interface (ABI) describes how the signature of a Lean declaration is encoded as a native calling convention.
It is based on the standard C ABI and calling convention of the target platform.
For a Lean declaration marked with either @[extern "sym"] or @[export sym] for some symbol name sym, let α₁ → ... → αₙ → β be the normalized declaration's type.
If n is 0, the corresponding C declaration is
extern s sym;
where s is the C translation of β as specified in the next section.
In the case of an @[extern] definition, the symbol's value is guaranteed to be initialized only after calling the Lean module's initializer or that of an importing module; see Initialization.
If n is greater than 0, the corresponding C declaration is
s sym(t₁, ..., tₘ);
where the parameter types tᵢ are the C translation of the αᵢ as in the next section.
In the case of @[extern] all irrelevant types are removed first; see next section.
Translating Types from Lean to C
-
The integer types
UInt8, ...,UInt64,USizeare represented by the C typesuint8_t, ...,uint64_t,size_t, respectively -
Charis represented byuint32_t -
Floatis represented bydouble -
An enum inductive type of at least 2 and at most 2^32 constructors, each of which with no parameters, is represented by the first type of
uint8_t,uint16_t,uint32_tthat is sufficient to represent all constructor indices.For example, the type
Boolis represented asuint8_twith values0forfalseand1fortrue. -
Decidable αis represented the same way asBool -
An inductive type with a trivial structure, that is,
- it is none of the types described above
- it is not marked
unsafe - it has a single constructor with a single parameter of relevant type
is represented by the representation of that parameter's type.
For example,
{ x : α // p }, theSubtypestructure of a value of typeαand an irrelevant proof, is represented by the representation ofα. Similarly, the signed integer typesInt8, ...,Int64,ISizeare also represented by the unsigned C typesuint8_t, ...,uint64_t,size_t, respectively, because they have a trivial structure. -
NatandIntare represented bylean_object *. Their runtime values is either a pointer to an opaque bignum object or, if the lowest bit of the "pointer" is 1 (lean_is_scalar), an encoded unboxed natural number or integer (lean_box/lean_unbox). -
A universe
Sort u, type constructor... → Sort u, or propositionp : Propis irrelevant and is either statically erased (see above) or represented as alean_object *with the runtime valuelean_box(0) -
Any other type is represented by
lean_object *. Its runtime value is a pointer to an object of a subtype oflean_object(see the "Inductive types" section below) or the unboxed valuelean_box(cidx)for thecidxth constructor of an inductive type if this constructor does not have any relevant parameters.Example: the runtime value of
u : Unitis alwayslean_box(0).
Inductive types
For inductive types which are in the fallback lean_object * case above and not trivial constructors, the type is stored as a lean_ctor_object, and lean_is_ctor will return true. A lean_ctor_object stores the constructor index in the header, and the fields are stored in the m_objs portion of the object.
The memory order of the fields is derived from the types and order of the fields in the declaration. They are ordered as follows:
- Non-scalar fields stored as
lean_object * - Fields of type
USize - Other scalar fields, in decreasing order by size
Within each group the fields are ordered in declaration order. Warning: Trivial wrapper types still count toward a field being treated as non-scalar for this purpose.
- To access fields of the first kind, use
lean_ctor_get(val, i)to get theith non-scalar field. - To access
USizefields, uselean_ctor_get_usize(val, n+i)to get theith usize field andnis the total number of fields of the first kind. - To access other scalar fields, use
lean_ctor_get_uintN(val, off)orlean_ctor_get_usize(val, off)as appropriate. Hereoffis the byte offset of the field in the structure, starting atn*sizeof(void*)wherenis the number of fields of the first two kinds.
For example, a structure such as
structure S where
ptr_1 : Array Nat
usize_1 : USize
sc64_1 : UInt64
ptr_2 : { x : UInt64 // x > 0 } -- wrappers don't count as scalars
sc64_2 : Float -- `Float` is 64 bit
sc8_1 : Bool
sc16_1 : UInt16
sc8_2 : UInt8
sc64_3 : UInt64
usize_2 : USize
ptr_3 : Char -- trivial wrapper around `UInt32`
sc32_1 : UInt32
sc16_2 : UInt16
would get re-sorted into the following memory order:
S.ptr_1-lean_ctor_get(val, 0)S.ptr_2-lean_ctor_get(val, 1)S.ptr_3-lean_ctor_get(val, 2)S.usize_1-lean_ctor_get_usize(val, 3)S.usize_2-lean_ctor_get_usize(val, 4)S.sc64_1-lean_ctor_get_uint64(val, sizeof(void*)*5)S.sc64_2-lean_ctor_get_float(val, sizeof(void*)*5 + 8)S.sc64_3-lean_ctor_get_uint64(val, sizeof(void*)*5 + 16)S.sc32_1-lean_ctor_get_uint32(val, sizeof(void*)*5 + 24)S.sc16_1-lean_ctor_get_uint16(val, sizeof(void*)*5 + 28)S.sc16_2-lean_ctor_get_uint16(val, sizeof(void*)*5 + 30)S.sc8_1-lean_ctor_get_uint8(val, sizeof(void*)*5 + 32)S.sc8_2-lean_ctor_get_uint8(val, sizeof(void*)*5 + 33)
Borrowing
By default, all lean_object * parameters of an @[extern] function are considered owned, i.e. the external code is passed a "virtual RC token" and is responsible for passing this token along to another consuming function (exactly once) or freeing it via lean_dec.
To reduce reference counting overhead, parameters can be marked as borrowed by prefixing their type with @&.
Borrowed objects must only be passed to other non-consuming functions (arbitrarily often) or converted to owned values using lean_inc.
In lean.h, the lean_object * aliases lean_obj_arg and b_lean_obj_arg are used to mark this difference on the C side.
Return values and @[export] parameters are always owned at the moment.
Initialization
When including Lean code as part of a larger program, modules must be initialized before accessing any of their declarations. Module initialization entails
- initialization of all "constants" (nullary functions), including closed terms lifted out of other functions
- execution of all
[init]functions - execution of all
[builtin_init]functions, if thebuiltinparameter of the module initializer has been set
The module initializer is automatically run with the builtin flag for executables compiled from Lean code and for "plugins" loaded with lean --plugin.
For all other modules imported by lean, the initializer is run without builtin.
Thus [init] functions are run iff their module is imported, regardless of whether they have native code available or not, while [builtin_init] functions are only run for native executable or plugins, regardless of whether their module is imported or not.
lean uses built-in initializers for e.g. registering basic parsers that should be available even without importing their module (which is necessary for bootstrapping).
The initializer for module A.B is called initialize_A_B and will automatically initialize any imported modules.
Module initializers are idempotent (when run with the same builtin flag), but not thread-safe.
Together with initialization of the Lean runtime, you should execute code like the following exactly once before accessing any Lean declarations:
void lean_initialize_runtime_module();
void lean_initialize();
lean_object * initialize_A_B(uint8_t builtin, lean_object *);
lean_object * initialize_C(uint8_t builtin, lean_object *);
...
lean_initialize_runtime_module();
//lean_initialize(); // necessary (and replaces `lean_initialize_runtime_module`) if you (indirectly) access the `Lean` package
lean_object * res;
// use same default as for Lean executables
uint8_t builtin = 1;
res = initialize_A_B(builtin, lean_io_mk_world());
if (lean_io_result_is_ok(res)) {
lean_dec_ref(res);
} else {
lean_io_result_show_error(res);
lean_dec(res);
return ...; // do not access Lean declarations if initialization failed
}
res = initialize_C(builtin, lean_io_mk_world());
if (lean_io_result_is_ok(res)) {
...
//lean_init_task_manager(); // necessary if you (indirectly) use `Task`
lean_io_mark_end_initialization();
In addition, any other thread not spawned by the Lean runtime itself must be initialized for Lean use by calling
void lean_initialize_thread();
and should be finalized in order to free all thread-local resources by calling
void lean_finalize_thread();
@[extern] in the Interpreter
The interpreter can run Lean declarations for which symbols are available in loaded shared libraries, which includes @[extern] declarations.
Thus to e.g. run #eval on such a declaration, you need to
- compile (at least) the module containing the declaration and its dependencies into a shared library, and then
- pass this library to
lean --load-dynlib=to run codeimporting this module.
Note that it is not sufficient to load the foreign library containing the external symbol because the interpreter depends on code that is emitted for each @[extern] declaration.
Thus it is not possible to interpret an @[extern] declaration in the same file.
See tests/compiler/foreign for an example.